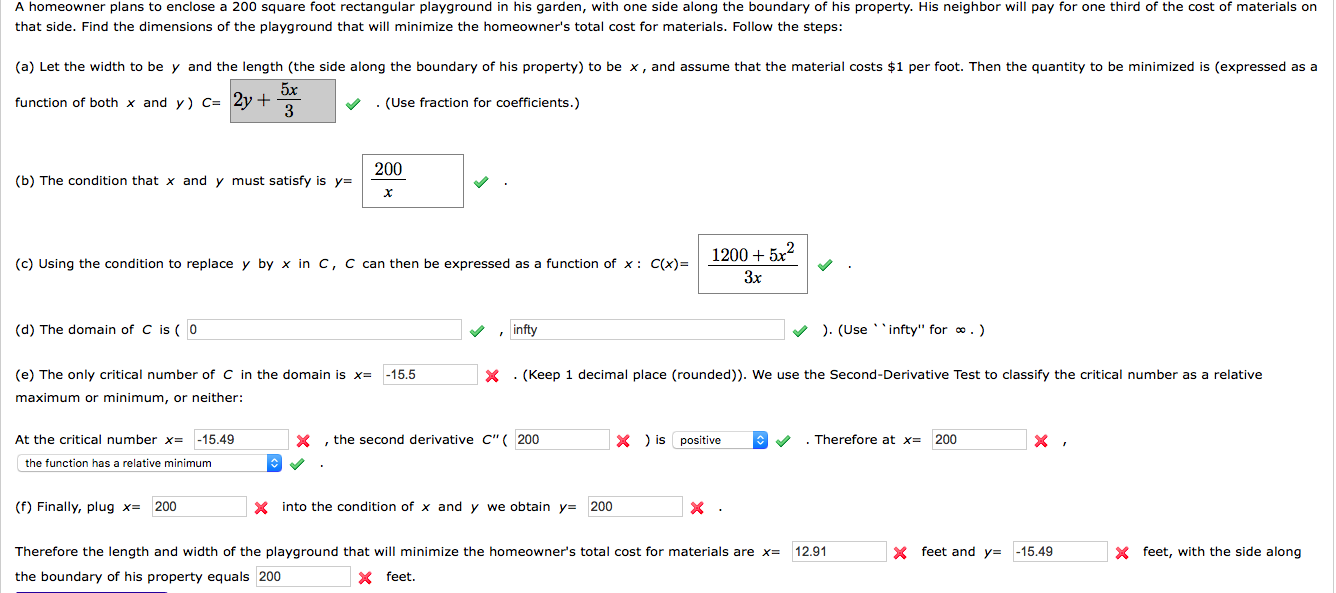
A homeowner plans to enclose a 200 square foot rectangular playground In his garden. with one side along the boundary of his property. His neighbor will pay for one third of the cost of materials on that side. Find the dimensions of the playground that will minimize the homeowner's total cost for materials. Follow the steps: (a) Let the width to be y and the length (the side along the boundary of his property) to be x , and assume that the material costs $1 per foot. Then the quantity to be minimized ls (expressed as a function of both x and y) C:- - f . (Use flaction for coefcients.) (b) The condition that x and 5/ must satisfy is y:- 1: 2 (c) Using the condition to replace y by x In C, C can then be expressed as a function of x: C(x)= % (d) The domain of C ls( D J , iny (e) The only critical number of C in the domain Is x: -15.5 x maximum or minimum, or neither: J ). (Use ' 'ln&y" for m.) . (Keep 1 decimal place (roundedjj. We use the Second-Derivative Test to classify the critical number as a relative x )is positive 3 . Therefore at x: 200 At the critical number x: 45.49 x , the second derivative C"( 200 the lunction has a relative minimum a J (f) Finally, plug x= 200 x into the condition of x and y we obtain y= 200 X Therefore the length and width of the playground that will minimize the homeowner's total cost for materials are x: 12.91 the boundary of his property equals 200 x feet. X x feet and y: 45.49 x feet, with the side along