A.If L is a language, then L + is defined to be {w1 wn|n 1 and wi L for 1 i n}. (The difference between L + and L is that is automatically in L , while is in L + if and only if it is in L.) Prove that the context-free languages are closed under the + operation.

B. Read Definition 2.8, Theorem 2.9 and Example 2.10 in the textbook (third edition) concerning Chomsky Normal Form and then put the following grammar into Chomsky Normal Form. S T aT aT T aT b|bT a|T T|

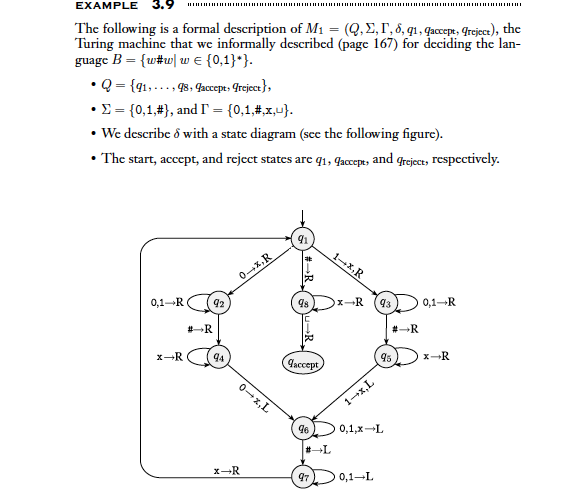
State diagram for Turing machine Mi In Figure 3.10, which depicts the state diagram of TM Mi, you will find the label 0,1R on the transition going from ga to itself. That label means that thc machine stays in qs and moves to the right when it reads a O or a 1 in state qs. It docsn't change the symbol on the tapc. Stage 1 is implemented by states q1 through qr, and stage 2 by the remaining states. To simplify the figure, we don't show the reject state or the transitions going to the reject state. Those transitions occur implicitly whenever a state lacks an outgoing transition for a particular symbol. Thus because in state qs no outgoing arrow with a # is present, if a # occurs under the head when the machine is in state qs, it goes to state grejecz. For completeness, we say that the head moves right in cach of these transitions to the reject state