a) If X = X(G,C) is a Cayley graph, then Aut(X) contains a subgroup isomorphic to G?

b) the 5-cycle is a Cayley Graph X = (G,C) for some group G and set C.

c) Draw out the Cayley graph X (G,C)

(please see more details in attachment, thank you)

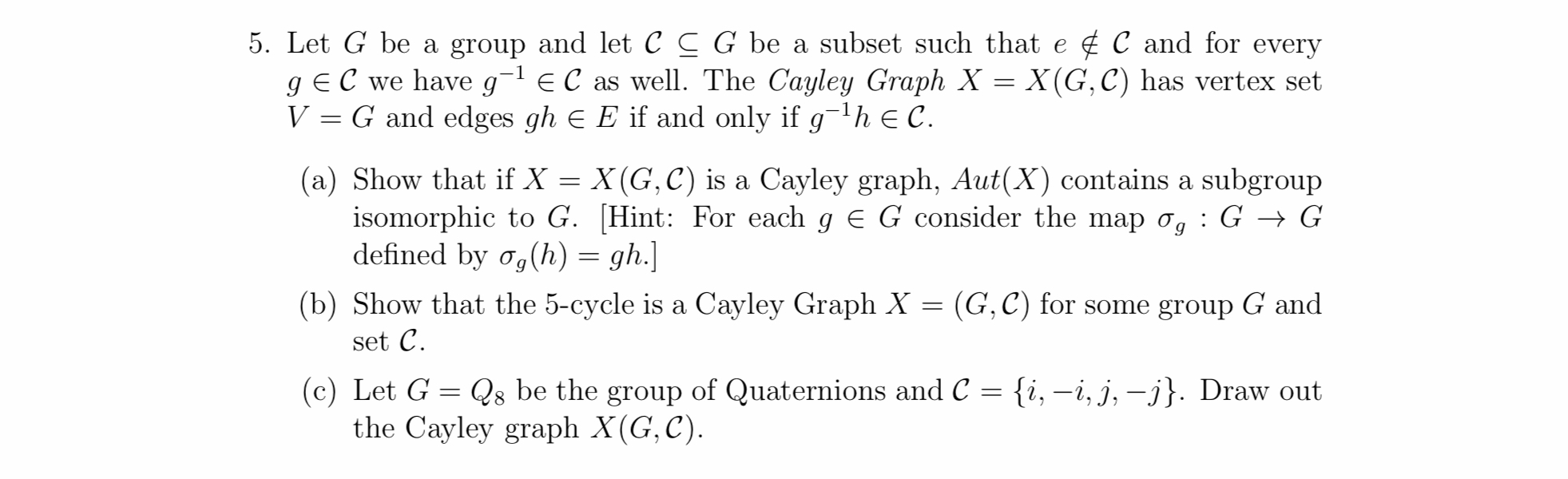
5. Let G be a group and let C C G be a subset such that e e C and for every g EC we have g- E C as well. The Cayley Graph X = X(G, C) has vertex set V = G and edges gh E E if and only if g-1h E C. (a) Show that if X = X(G, C) is a Cayley graph, Aut(X) contains a subgroup isomorphic to G. [Hint: For each g E G consider the map o, : G - G defined by o,(h) = gh.] (b) Show that the 5-cycle is a Cayley Graph X = (G, C) for some group G and set C. (c) Let G = Qg be the group of Quaternions and C = {i, -i, j, -j}. Draw out the Cayley graph X (G, C)