$($a$)$ If you haven't already done so$,$ enter the following commands:

f$=0($t$,$y$),0\mathrm{.}5*$y;

t$=$ inspace $(0,2\mathrm{.}25,100)$;y$=-4*$exp$(0\mathrm{.}5*$t$)$; $\%$define exact solution of the ODE

$[$t$90,$y$90]=$euler$($f$,[0,2\mathrm{.}25],4,90)$; $\%$solve the ODE uaing Euler$($ w$)/(90)$ atepa

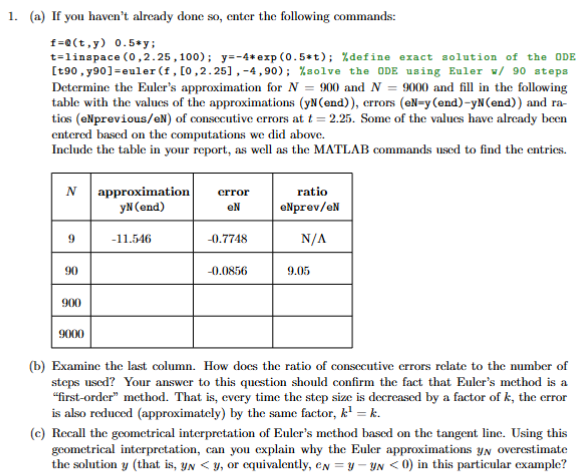
Determine the Euler's approximation for N$=900$ and N$=9000$eN$=$y $($end$)-$yN $($end$)$t$=2\mathrm{.}25.$ Some of the values have already been

entered based on the computations we did above.

Include the table in your report, as well as the MATLAB commands used to find the entries.

$($b$)$ Examine the last column. How does the ratio of consecutive errors relate to the number of

steps used? Your answer to this question should confirm the fact that Euler's method is a

"first$-$order" method. That is$,$ every time the step size is decreased by a factor of k$,$ the error

is also reduced $($approximately$)$ by the same factor, k$^(1)=$k$.$

$($c$)$ Recall the geometrical interpretation of Euler's method based on the tangent line. Using this

geometrical interpretation, can you explain why the Euler approximations y$\_($N$)$ overestimate

the solution ye$\_($N$)=$y$-$y$\_($N$)<mn>0</mn>$y$\_($N$),$ or equivalently, e$\_($N$)=$y$-$y$\_($N$)<mn>0</mn>$