Question: (a) Let p be an odd prime and G a group of order 2p. Show that G is either cyclic i. e. G=Z, or
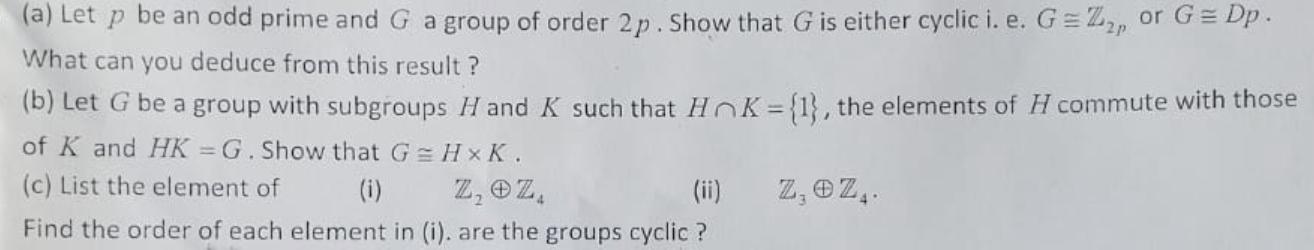
(a) Let p be an odd prime and G a group of order 2p. Show that G is either cyclic i. e. G=Z, or G = Dp. What can you deduce from this result? (b) Let G be a group with subgroups H and K such that HK = {1}, the elements of H commute with those of K and HK = G. Show that G = H K. (c) List the element of (i) Z, OZA (ii) Z, Z. Find the order of each element in (i). are the groups cyclic ?
Step by Step Solution
3.52 Rating (152 Votes )
There are 3 Steps involved in it
a To prove that a group G of order 2p where p is an odd prime is either cyclic ie GZ 2p or isomorphic to the dihedral group of order 2p ie GD p well use Sylows theorems First lets denote n p as the nu... View full answer

Get step-by-step solutions from verified subject matter experts


