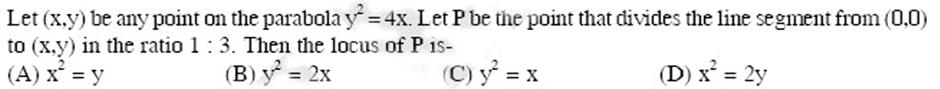
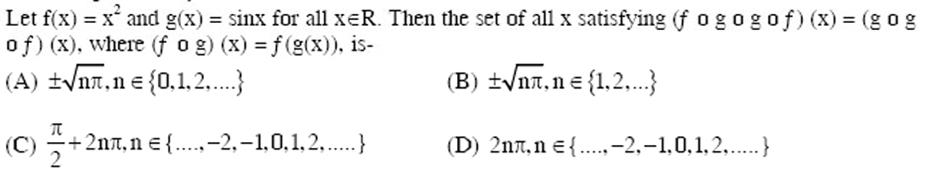
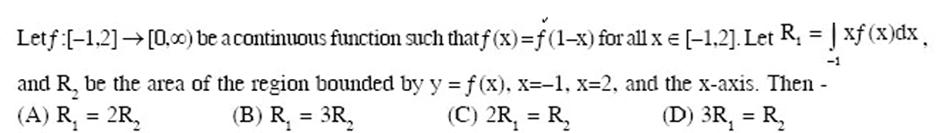
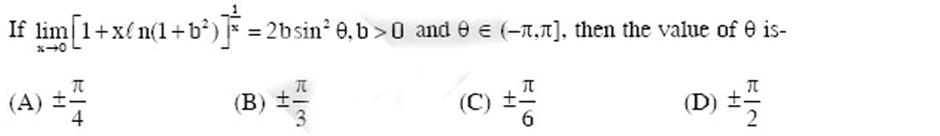
(A) Let P(6, 3) be a point on the hyperbola x-axis at (9,0), then the eccentricity of the hyperbola is - F (C) 2 (B) 44 2/2 X* a b -=1. If the normal at the point P intersects the (D) 3 Let (x,y) be any point on the parabola y=4x. Let P be the point that divides the line segment from (0,0) to (x,y) in the ratio 1:3. Then the locus of P is- (B) y = 2x (D) x = 2y (A) x = y (C) y = x Let f(x) = x and g(x) = sinx for all x=R. Then the set of all x satisfying (f og o gof)(x) = (gog of) (x), where (fog)(x) = f(g(x)), is- (A) n,ne {0,1,2,...} (B) n, n = {1,2,...} (D) 2nt, n = {...-2,-1,0, 1, 2,...} (C) +2nt.n {....-2,-1,0,1,2...... Letf:[1,2] [0,00) be a continuous function such that f(x) = f (1-x) for all x = [-1,2]. Let R = | xf (x)dx -1 and R, be the area of the region bounded by y = f(x), x=-1, x=2, and the x-axis. Then - (A) R = 2R (C) 2R = R (D) 3R = R (B) R = 3R If lim[1+x{n(1+b)] =2bsin 0,b>0 and 0 (-], then the value of 0 is- 1+ K|4 (A) - (B) +1 TU 3 (C) +1 H|6 (D) +1 EIN