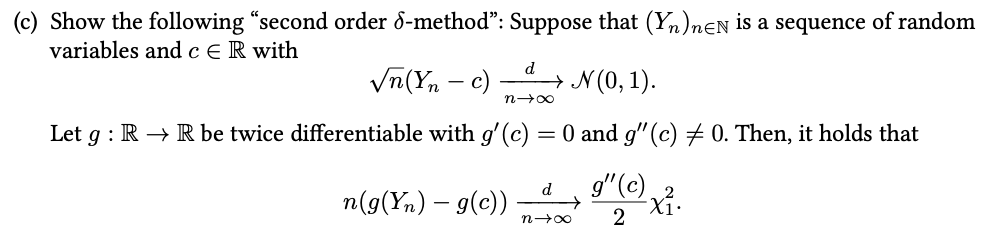
(a) Let X = (X1, X2) be a random vector with X N ght, 2), where we he 21)- Find the distribution on = X1 + 2X2 and of Z = (X1 + X2, X2). (b) Consider U N W\"), 1) and R N Berg), independent from U. Set Show that V N JV\"), 1). Explain that Cov[U, V] = 0, and that U and V are not independent. (c) Show the following "second order o-method": Suppose that (Yn )new is a sequence of random variables and c E R with Vn( Yn - c) d N ( 0 , 1 ) . Let g : R - R be twice differentiable with g'(c) = 0 and g"(c) * 0. Then, it holds that n(g(Yn) - g(c)) d g" (c) n-+00 2 X3