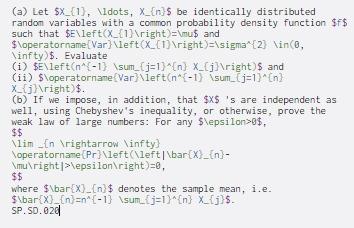
(a) Let $x_{1}, \ldots, X_n be identically distributed random variables with a common probability density function $f$ such that $E\left(x_{1} ight) = \mu$ and $\operatorname[Var}\left(x) ight)=\sigma'{2] Ninc, \infty$. Evaluate (i) $E\left(n^-1} \sum_(j=1}^{n} X_{j} ight) and (ii) $\operatorname[Var}\left(n-1) sum_(j=1}^{n} X_{j} ight)$. (b) If we impose, in addition, that $X$ 's are independent as well, using Chebyshev's inequality, or otherwise, prove the weak law of large numbers: For any $\epsilon>$ $$ \limin ightarrow \infty) \operatorname Pr}\left(\left\bar{X}_{n)- mu ight|>\epsilon ight)=0, $$ where $\bar)..(n) $ denotes the sample mean, i.e. $\bar{X}_{n}={-1} \sum _{j=1}^{n} X_{j}$ SP.S0.020