Question: A linear programming computer package is needed. Romans Food Market, located in Saratoga, New York, carries a variety of specialty foods from around the world.

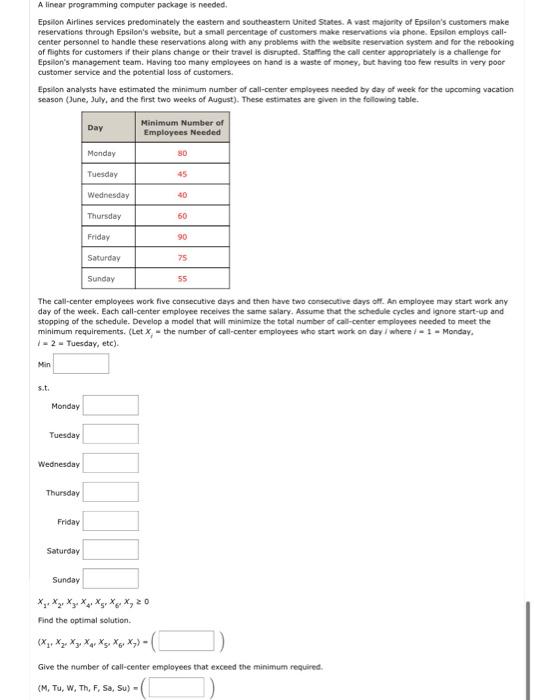

A linear programming computer package is needed. Romans Food Market, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilian Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City, Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions of each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Romans would like to place an order for the Brazilian and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular coffee and 400 pounds of Romans DeCaf coffee. The production cost is $0.80 per pound for the Regular blend. Because of the extra steps required to produce DeCaf, the production cost for the DeCaf blend is $1.05 per pound. Packaging costs for both products are $0.25 per pound. (a) Formulate a linear programming model that can be used to determine the pounds of Brazilian Naturai and Colombian Mild that will maximize the total contribution to profit. (Let BR= pounds of Brazilian beans purchased to produce Regular, BD = pounds of Brazilian beans purchased to produce DeCaf, CR = pounds of Colombian beans purchased to produce Regular, and CD pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular % constraint DeCaf \% constraint Pounds of Regular Pounds of DeCaf (b) What is the optimal solution? (BR,BD,CR,CD)=( (c) What is the contribution to profit (in $ )? (Round your answer to two decimal places.) $ A linear programming computer pockage is needed. Epsilon Airlines services predominately the eastern and sovtheastern United States. A vast majoriky of Epsilen's cuatemers make reservations through Epsilon's website, but a small percentage of customers make reservations wia phene. Epsilon employs callcenter personnel to handle these reservations along with any problems with the website reservation system and for the rebooking of fights for customers if their plans change or their travel is diarupted. Staffing the call center appropriately is a challenge for Epsilon's management team. Having too many employees on hand is a waste ef money, but having too few results in very poor customer service and the potential loss of customers. Epsilon analysts have estimated the minimum number of call-center employees needed by day of week for the upcoming vacation season (June, Jully, and the first two weeks of August). These estimates are given in the foillowing table. The call-center employees work five cansecutive days and then have two consecutive days off. An employee may start work any day of the week. Each call-center employee receives the same salary, Assume that the schedule cycles and ignore start-up and stopping of the schedule. Develop a model that will minimize the total number of call-center employees needed to meet the minimum requirements. (Let xj= the number of call-center employees who start work on day i where f=1 = Monday. 1=2 = Tuesday, etc). Min 5.t. Monday Tuesday Wednesday Thursday Friday Saturday Sunday x1,x2,x3,x4,x5,x6,x30 Find the optimal solution. (x1,x2,x3,x4,x5,x6,x7)=( Give the number of call-center employees that exceed the minimum required. (M,Tu,W,Th,F,,Sa,Su)=( Romans Food Market, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilian Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City. Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions of each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Romans would like to place an order for the Brazilian and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular coffee and 400 pounds of Romans DeCaf coffee. The production cost is $0.80 per pound for the Regular blend. Because of the extra steps required to produce DeCaf, the production cost for the DeCaf blend is $1.05 per pound. Packaging costs for both products are $0.25 per pound. (a) Formulate a linear programming model that can be used to determine the pounds of Brazilian Natural and Colombian Mild that will maximize the total contribution to profit, (Let BR = pounds of Brazilian beans purchased to produce Regular, BD = pounds of Brazilian beans purchased to produce DeCaf, CR= pounds of Colombian beans purchased to produce Regular, and CO= pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular \% constraint DeCaf \% constraint Pounds of Regular Pounds of DeCaf (b) What is the optimal solution? (BR,BD,CR,CD)=( (c) What is the contribution to profit (in $ )? (Round your answer to two decimal places.) $ A linear programming computer package is needed. Romans Food Market, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilian Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City, Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions of each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Romans would like to place an order for the Brazilian and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular coffee and 400 pounds of Romans DeCaf coffee. The production cost is $0.80 per pound for the Regular blend. Because of the extra steps required to produce DeCaf, the production cost for the DeCaf blend is $1.05 per pound. Packaging costs for both products are $0.25 per pound. (a) Formulate a linear programming model that can be used to determine the pounds of Brazilian Naturai and Colombian Mild that will maximize the total contribution to profit. (Let BR= pounds of Brazilian beans purchased to produce Regular, BD = pounds of Brazilian beans purchased to produce DeCaf, CR = pounds of Colombian beans purchased to produce Regular, and CD pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular % constraint DeCaf \% constraint Pounds of Regular Pounds of DeCaf (b) What is the optimal solution? (BR,BD,CR,CD)=( (c) What is the contribution to profit (in $ )? (Round your answer to two decimal places.) $ A linear programming computer pockage is needed. Epsilon Airlines services predominately the eastern and sovtheastern United States. A vast majoriky of Epsilen's cuatemers make reservations through Epsilon's website, but a small percentage of customers make reservations wia phene. Epsilon employs callcenter personnel to handle these reservations along with any problems with the website reservation system and for the rebooking of fights for customers if their plans change or their travel is diarupted. Staffing the call center appropriately is a challenge for Epsilon's management team. Having too many employees on hand is a waste ef money, but having too few results in very poor customer service and the potential loss of customers. Epsilon analysts have estimated the minimum number of call-center employees needed by day of week for the upcoming vacation season (June, Jully, and the first two weeks of August). These estimates are given in the foillowing table. The call-center employees work five cansecutive days and then have two consecutive days off. An employee may start work any day of the week. Each call-center employee receives the same salary, Assume that the schedule cycles and ignore start-up and stopping of the schedule. Develop a model that will minimize the total number of call-center employees needed to meet the minimum requirements. (Let xj= the number of call-center employees who start work on day i where f=1 = Monday. 1=2 = Tuesday, etc). Min 5.t. Monday Tuesday Wednesday Thursday Friday Saturday Sunday x1,x2,x3,x4,x5,x6,x30 Find the optimal solution. (x1,x2,x3,x4,x5,x6,x7)=( Give the number of call-center employees that exceed the minimum required. (M,Tu,W,Th,F,,Sa,Su)=( Romans Food Market, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilian Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City. Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions of each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Romans would like to place an order for the Brazilian and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular coffee and 400 pounds of Romans DeCaf coffee. The production cost is $0.80 per pound for the Regular blend. Because of the extra steps required to produce DeCaf, the production cost for the DeCaf blend is $1.05 per pound. Packaging costs for both products are $0.25 per pound. (a) Formulate a linear programming model that can be used to determine the pounds of Brazilian Natural and Colombian Mild that will maximize the total contribution to profit, (Let BR = pounds of Brazilian beans purchased to produce Regular, BD = pounds of Brazilian beans purchased to produce DeCaf, CR= pounds of Colombian beans purchased to produce Regular, and CO= pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular \% constraint DeCaf \% constraint Pounds of Regular Pounds of DeCaf (b) What is the optimal solution? (BR,BD,CR,CD)=( (c) What is the contribution to profit (in $ )? (Round your answer to two decimal places.) $
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


