A linear programming model was used to minimize costs.

MIN 4X₁+4X₂+6X₃

ST X₁+X₂+X₃

2X₁+5X₂+4X₃>=280

2X₁+2X₂+4X₃>=320

1) What is the optimal solution?

X₁ = 1

X₂ = 1

X₃ = 0 Objective Function = 480.00

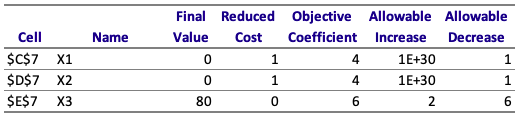
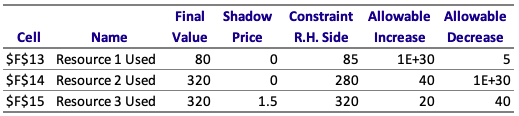
2) Based on the Sensitivity Report, what is the constraint, if any, are binding constraints at optimal solution? Resource 1, Resource 2, Resource 3, or none. I chose resource 3, but I'm not sure how accurate that is.

3) How should shadow price for binding constraint in the problem be interpretended?

\begin{tabular}{ccrr} \hline Cell & Name & Original Value & Final Value \\ \hline$C$10 & Objective Function MIN X1 & 0.00 & 480.00 \\ \hline \end{tabular} \begin{tabular}{ccrrrrrr} \hline Cell & & Name & Final Value & Reduced Cost & Objective Coefficient & Allowable Increase & Allowable Decrease \\ \hline$7 & X1 & 0 & 1 & 4 & 1E+30 & 1 \\ \hline$D$7 & X2 & & 0 & 1 & 4 & 1E+30 & 1 \\ \hline$E$7 & X3 & & 80 & 0 & 6 & 2 & 6 \\ \hline \end{tabular} \begin{tabular}{ccrr} \hline Cell & Name & Original Value & Final Value \\ \hline$C$10 & Objective Function MIN X1 & 0.00 & 480.00 \\ \hline \end{tabular} \begin{tabular}{ccrrrrrr} \hline Cell & & Name & Final Value & Reduced Cost & Objective Coefficient & Allowable Increase & Allowable Decrease \\ \hline$7 & X1 & 0 & 1 & 4 & 1E+30 & 1 \\ \hline$D$7 & X2 & & 0 & 1 & 4 & 1E+30 & 1 \\ \hline$E$7 & X3 & & 80 & 0 & 6 & 2 & 6 \\ \hline \end{tabular}