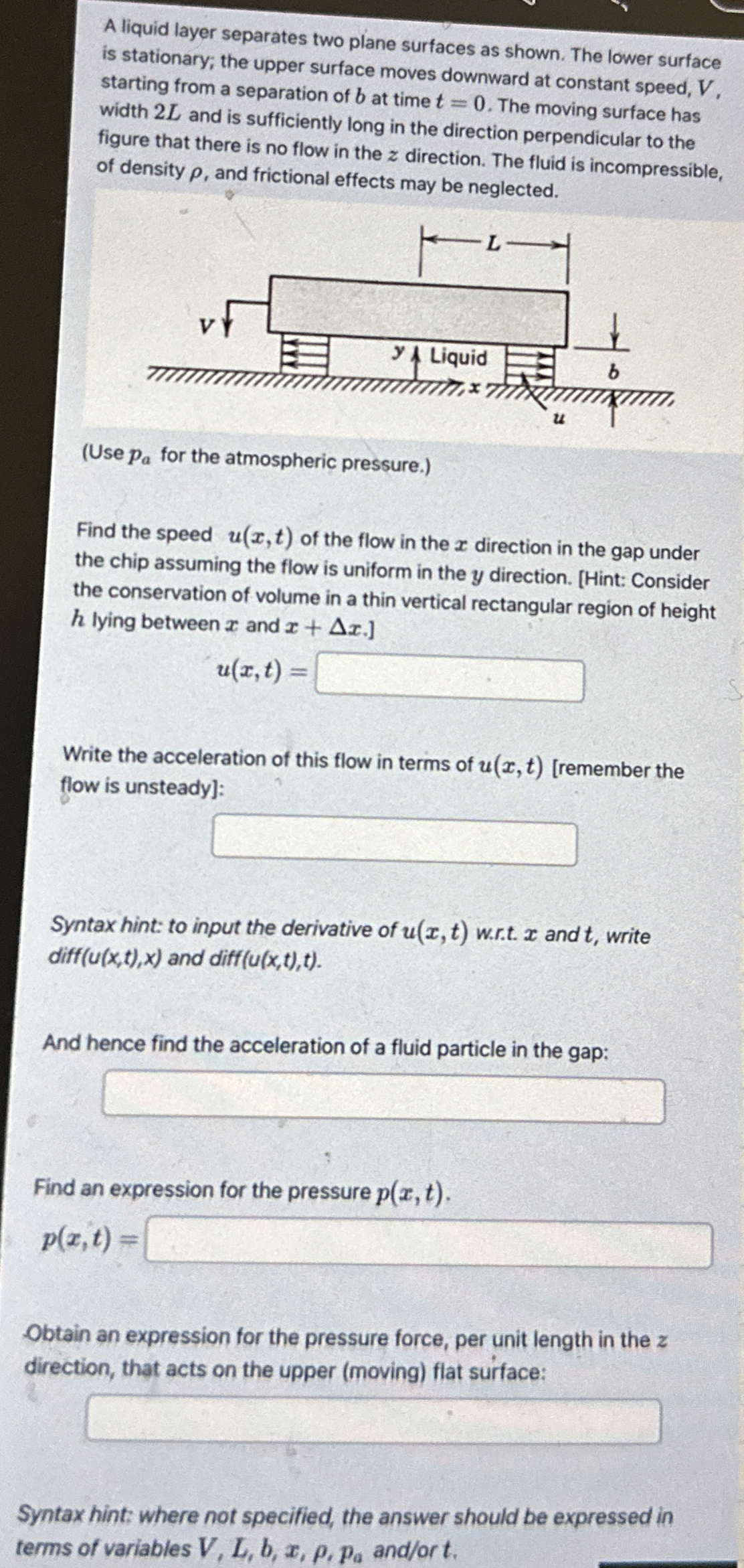
A liquid layer separates two plane surfaces as shown. The lower surface is stationary; the upper surface moves downward at constant speed, $V,$ starting from a separation of $b$ at time $t=0.$ The moving surface has width $2L$ and is sufficiently long in the direction perpendicular to the figure that there is no flow in the $z$ direction. The fluid is incompressible, of density $,$ and frictional effects may be neglected.

$($Use $p_a$ for the atmospheric pressure.$)$

Find the speed $u(x,t)$ of the flow in the $x$ direction in the gap under the chip assuming the flow is uniform in the $y$ direction. $[$Hint: Consider the conservation of volume in a thin vertical rectangular region of height $h$ lying between $x$ and $x+x.]$

$u(x,t)=$

Write the acceleration of this flow in terms of $u(x,t)[$remember the flow is unsteady$]$:

Syntax hint: to input the derivative of $u(x,t)$ w$.$r$.$t$.x$ and $t,$ write diff$(u(x,t),x)$ and diff $(u(x,t),t).$

And hence find the acceleration of a fluid particle in the gap:

Find an expression for the pressure $p(x,t).$

$p(x,t)=$

$$

Obtain an expression for the pressure force, per unit length in the $z$ direction, that acts on the upper $($moving$)$ flat surface:

Syntax hint: where not specified, the answer should be expressed in terms of variables $V,L,b,x,,p_a$ and$/$or $t.$