A machine part in the form a parallelopiped is deformed into the shape indicated by the dashed straight lines (small displacements). The displacements are given by the following relations: u= C1xyz, v=C2xyz, w=C3xyz

The back face GF is ?detached?. The coordinates of G* have displaced to (0.001, 0.001, 1.999), and the coordinates of F* are at (0.002, 1.002, 1.998). The position of point E* is still (1.504, 1.002, 1.996) as per the example.

a) Find the displacement relations for u, v and w.

b) Find the normal strain at the central point of the parallelepiped shape, in a direction emanating from the origin to point E

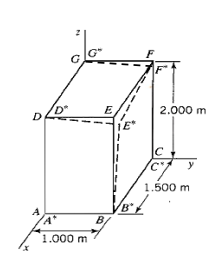
D D" A* 1.000 m E B 2.000 m C 1.500 m