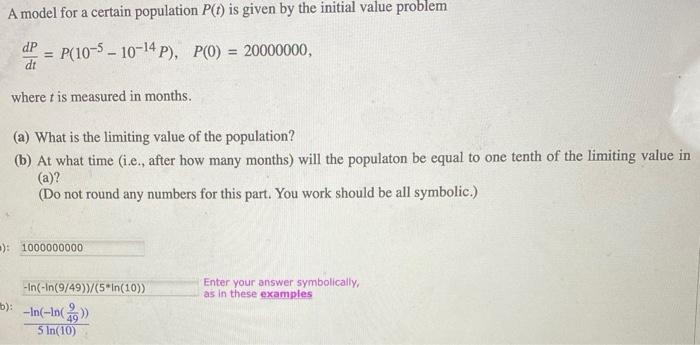
A model for a certain population P(t) is given by the initial value problem P(10-5-10-14 P), P(0) = 20000000, dP dt = where t is measured in months. (a) What is the limiting value of the population? (b) At what time (i.e., after how many months) will the populaton be equal to one tenth of the limiting value in (a)? (Do not round any numbers for this part. You work should be all symbolic.) ): 1000000000 -In(-In(9/49))/(5*In(10)) b): -In(-In()) 5 In(10) Enter your answer symbolically, as in these examples