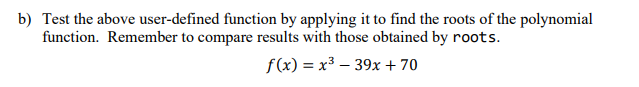
a) Modify the bisection method m-file to perform the false-position method, and discuss the differences between these two methods. The false-position formula/algorithm can be found in the lectures notes. (Basically just change one line in the bisection code on how to define "x") Rename the root finding user-defined function to FalsePos. Modify the code to return the approximate root, the number of iterations required to perform the calculation, and any other useful information for the user. b) Test the above user-defined function by applying it to find the roots of the polynomial function. Remember to compare results with those obtained by roots. f(x) = x3 39x + 70 c) Find the 10-th root of the number 15 (i.e. x 10 = 15) using both the bisection method and false position method. Use an initial bracket defined by a = 1 and b = 2. Print the results of each iteration and compare the convergence of the two methods. Which method converges faster? Look at a graph of the function and comment on why this method is expected to converge faster. bisection_part.mx + function [x, n] = bisection (fun, a, b, maxtol, maxitr) if nargin 0 error(['The function values at the bracket endpoints must differ in sign. ', 'This means that there is either no root or possibly an even number', 'of roots in the initial bracket.']) end fprintf(" Iter#\ta\t\t\tf(a)\t\tb\t\t\tf(b)\t\tx\t\t\tf(x) '); fprintf('i\t\tsf\t%f\t%f\t%[\t%f ',k, a, fun(a),b, fun (b)) while funx = fun (x); if abs (funx) = maxtol fprintf(' ') warning ("Maximum number of iterations reached before convergence') fprintf(" Solution not obtained in $d iterations. ',maxitr); ('No answer'); n = ('No answer'); end end