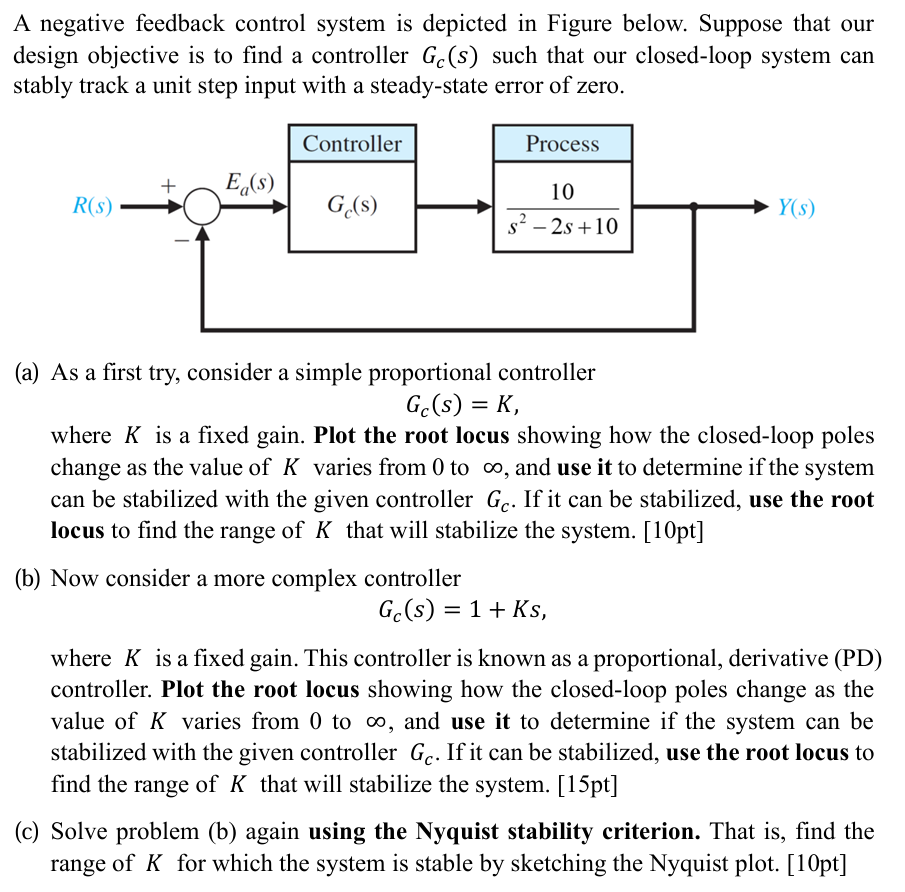
Question: A negative feedback control system is depicted in Figure below. Suppose that our design objective is to find a controller ( G _ {
A negative feedback control system is depicted in Figure below. Suppose that our design objective is to find a controller Gcs such that our closedloop system can stably track a unit step input with a steadystate error of zero.
a As a first try, consider a simple proportional controller
GcsK
where K is a fixed gain. Plot the root locus showing how the closedloop poles change as the value of K varies from to infty and use it to determine if the system can be stabilized with the given controller Gc If it can be stabilized, use the root locus to find the range of K that will stabilize the system. pt
b Now consider a more complex controller
GcsK s
where K is a fixed gain. This controller is known as a proportional, derivative PD controller. Plot the root locus showing how the closedloop poles change as the value of K varies from to infty and use it to determine if the system can be stabilized with the given controller Gc If it can be stabilized, use the root locus to find the range of K that will stabilize the system. pt
c Solve problem b again using the Nyquist stability criterion. That is find the range of K for which the system is stable by sketching the Nyquist plot. pt
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


