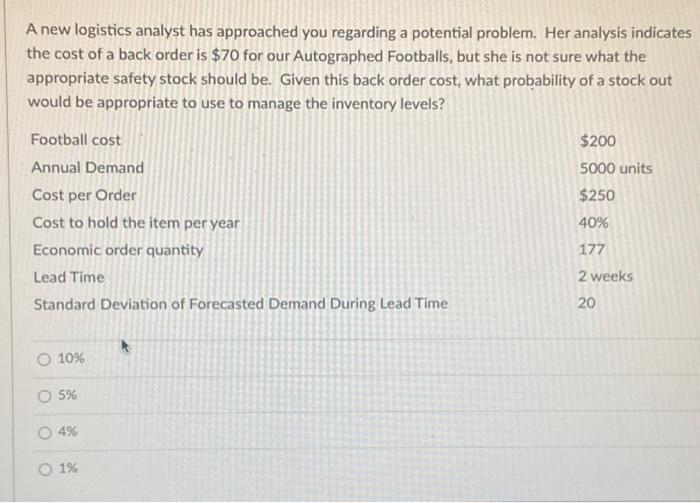
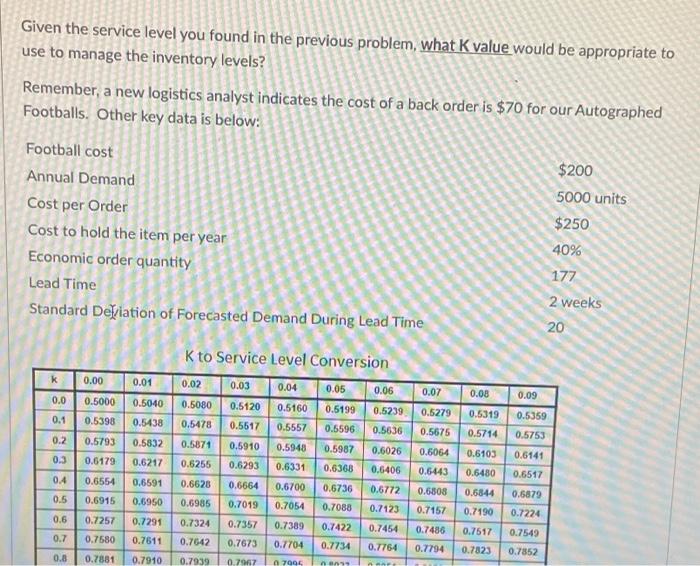
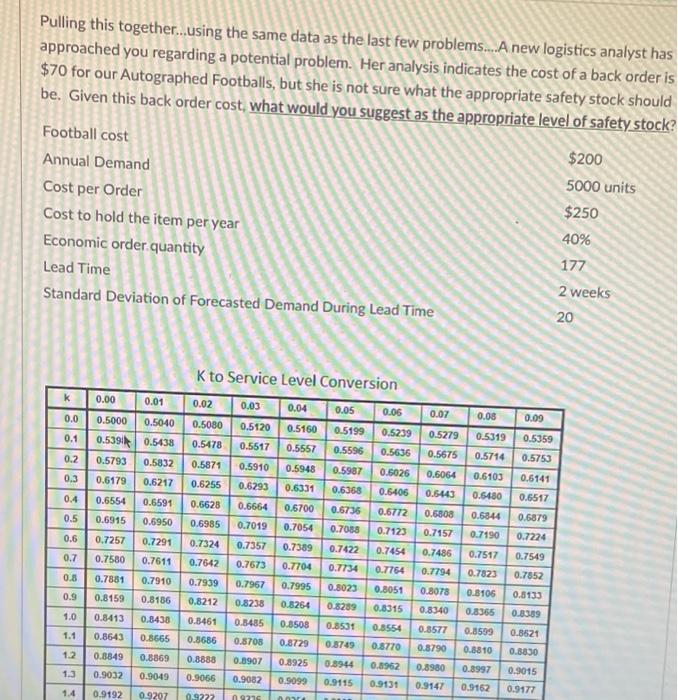
Question: A new logistics analyst has approached you regarding a potential problem. Her analysis indicates the cost of a back order is $70 for our Autographed

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


