Question: A normal population has mean = 37 and standard deviation = 8. (a) What proportion of the population is between 19 and 29? (b)

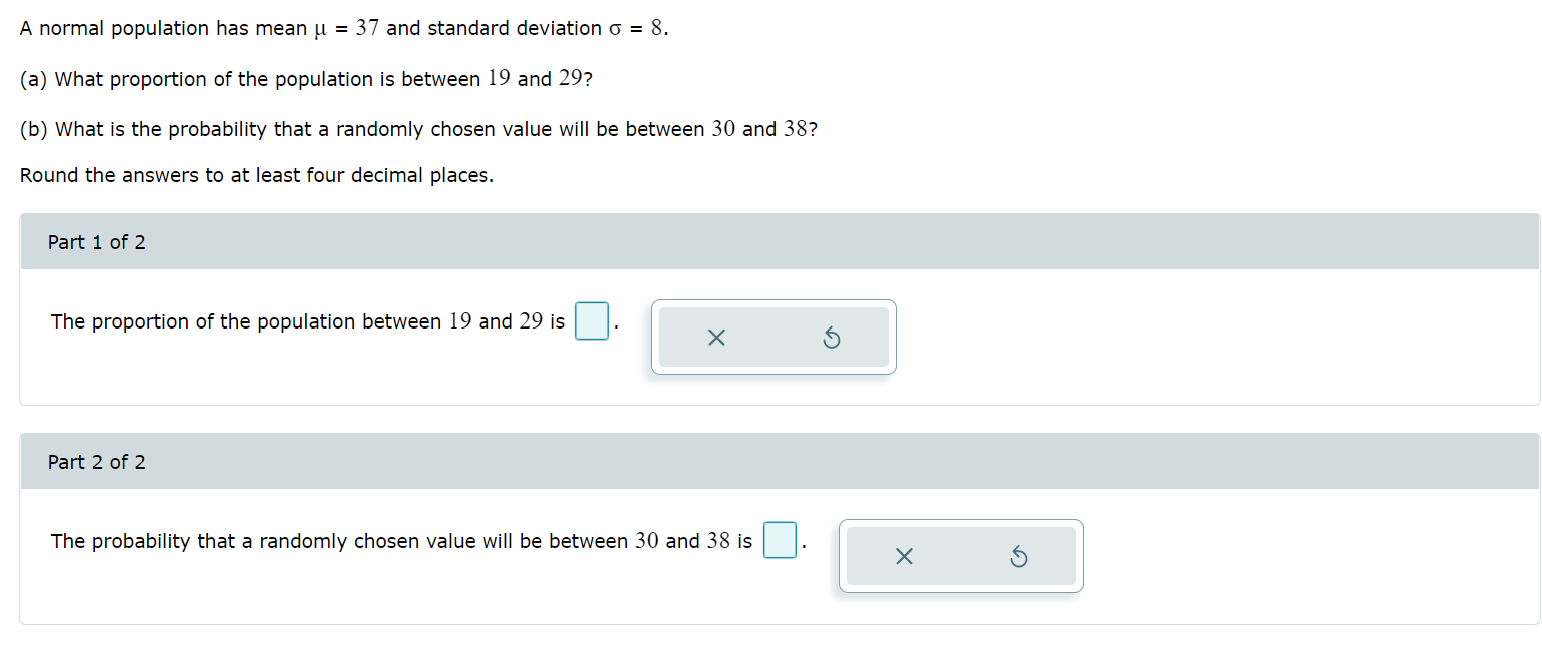
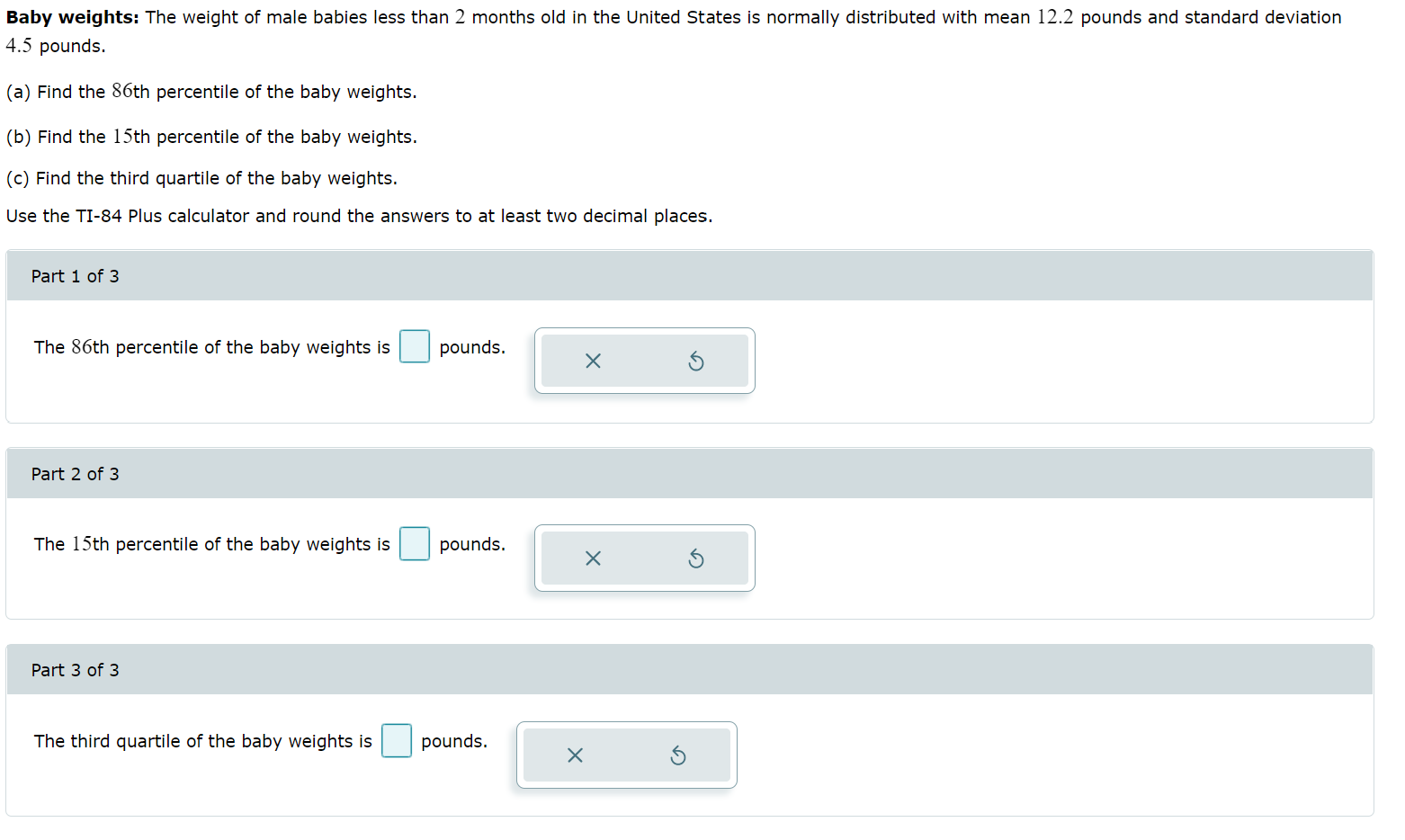
What is the probability that a randomly chosen value will be between

A normal population has mean = 37 and standard deviation = 8. (a) What proportion of the population is between 19 and 29? (b) What is the probability that a randomly chosen value will be between 30 and 38? Round the answers to at least four decimal places. Part 1 of 2 The proportion of the population between 19 and 29 is Part 2 of 2 The probability that a randomly chosen value will be between 30 and 38 is A normal population has mean = 51 and standard deviation = 7. What is the 85th percentile of the population? Use the TI-84 Plus calculator. Round the answer to at least one decimal place. The 85th percentile of the population is Baby weights: The weight of male babies less than 2 months old in the United States is normally distributed with mean 12.2 pounds and standard deviation 4.5 pounds. (a) Find the 86th percentile of the baby weights. (b) Find the 15th percentile of the baby weights. (c) Find the third quartile of the baby weights. Use the TI-84 Plus calculator and round the answers to at least two decimal places. Part 1 of 3 The 86th percentile of the baby weights is Part 2 of 3 pounds. The 15th percentile of the baby weights is pounds. Part 3 of 3 The third quartile of the baby weights is pounds.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Supply a valid technology formula for the given function. 7 1 37 3-9x

Given the following data, show that multiplying each score by a constant multiplies all measures of central tendency by that constant. 8 3 5 5 6 2

Use the upper bound technique manually to solve the following problem. Maximize Z = x1 + 3x2 2x3, Subject to and x1 ¥ 0, x2 ¥ 0, x3 ¥ 0. 2 2x 22 8 12 2

Apply Theorem 3 to calculate the matrix exponential e At for each of the matrices in Problems 35 through 40. A = 13 3 3 3 01 3 3 00 23 0002

The controller of Boom Box Sounds Inc. prepared the following product profitability report for management using activity-based costing methods for allocating both the factory overhead and the...

Explain why correctly owning assets is important to the personal finances of people, especially couples. AppendixLO1

In the article Dialyzable free cortisol after stimulation with synacthen published in the journal Clinical Biochemistry (Vogeser et al., 2002), the authors reported the raw data given in Table 6.9 on...

LRNA Company issued $300,000, 11%, 10-year bonds on January 1, 2015, for $318,694. This price resulted in an effective-interest rate of 10% on the bonds. Interest is payable semiannually on July 1...

The Walston Company is to be liquidated and has the following liabilities: Income taxes Notes payable (secured by land) Accounts payable Salaries payable (evenly divided between two employees) Bonds...

The Fire Free Company issued a 15 -year bond 2 years ago. The coupon rate is 5.4%. Interest payments are made every June 30th and December 31st. The bonds currently sell for 106% of par value....

3-37. In a motion capture study of a runner, one frame shows the subject support- ing her weight on one leg, as shown in Fig. P3.37. The length of the foot seg- ment (from ankle to toe) is 8 in. and...

Exhibit 12-1 A square of side 2 is removed from one corner of a square sandwich that has sides of length L. The center of mass of th remainder of the sandwich moves from C to C'. Use this exhibit to...

5. A consumer decides not to buy a VCR when her income is $20,000. However, when her income rises to $30,000, she decides to buy one. In a single diagram, draw the budget lines and indifference...

1. With loads A, B, C, and D applied as shown, find: (a) (6 points) The total moment about point O. (b) (4 points) The moment about the axis from O to A. If A 75 N, B=25 N, C=50 N, and D = 100 N. B B...

A lender encourages a borrower who receives a federally related mortgage loan from it to employ an attorney to perform the title searches and related settlement services in connection with their...

Starware Software was founded last year to develop software for gaming applications. The founder initially invested 5800,000 and received 12 million shares of stock. Starware now needs to raise a...

What are the two components of a company's income tax provision? What does each component represent about a company's income tax provision?

6. Let the transition probability matrix of a two-state Markov chain be given, as in Example 4.2, by P = 3 3 3 3 p 1 p 1 p p 3 3 3 3 Show by mathematical induction that P(n) = 3 3 3 3 3 1 2 + 1 2...

11. In Example 4.3, Gary was in a glum mood four days ago. Given that he hasnt felt cheerful in a week, what is the probability he is feeling glum today?

4. Consider a process {Xn,n = 0, 1,...} which takes on the values 0, 1, or 2. Suppose P{Xn+1 = j |Xn = i,Xn1 = in1,...,X0 = i0} = PI ij , when n is even PII ij , when n is odd where 2 j=0 PI ij = 2...