A normal random variable has an unknown mean and standard

deviation 2 if the probability that exceeds 7.5 is 0.8023, find

18 50 students take 10-points exam, 58 of them passed the exam;

if the distribution of the scores for all students is normal

distribution with mean is equal to 7 and standard deviation 2.

a. Find the number of students gets scores between 5 and 7.

b. What is the score for passing.

19 For the standard normal curve, the area that lies to the left of

1.13 is

A) 0.8708 B) 0.1292 C) 0.8907 D) 0.8485

Eight tennis players (call them A,B,C,D,E,G,F,H) are randomly assigned to start positions in a ladder tournament. Initially, position 1 plays position 2, position 3 plays

4, 5 plays 6 and 7 plays 8. Second round has 2 matches: winner of (1,2) match plays

winner of (3,4), and winner (5,6) plays winner(7,8). The winners of the two 2nd round

matches play each other in the final match. Player A wins against any of the others.

Player B always beats any opponent except player A. What is the probability that

player B wins the 2nd place trophy in the final match?

24. In a roomful of 30 people, what is the probability that at least two people have the

same birthday? Assume birthdays are uniformly distributed and there is no leap year

complication.

Google this - it's a classic problem, and several innovative presentations of the proper

calculations are available. Be sure to verify the accuracy of the solution(s) you find!!

25. A coach is training 15 girls. He wants to form 5 lines of 3 forwards each (left-wing,

center, and right-wing). Assume that the order of assigning these positions matters.

What is the probability that both Ann and May are in the same line?

26. What is the probability of receiving a 7 (3 letters, then 4 numbers) digit license plate

with a repeated letterumber?

27. What is the probability of having a license plate (3 letters, then 4 numbers) with either

all vowels OR consonances?

28. What is the probability of randomly selecting a bill from a wallet and getting a $20

bill out of a wallet with 2 tens, 3 fives, 4 twenties, and 7 ones?

29. What is the probability of getting a 70% or better on a 20 question multiple choice

test with 4 choices each, randomly guessing?

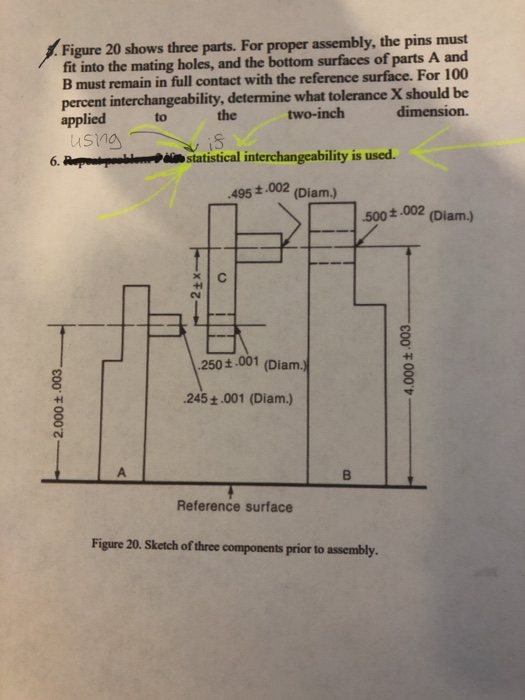
At University of West Georgia, 45% of the students take a Statistics class, 39% of the students take a Geography course, and 30% of the students take both Statistics and Geography classes. What is the probability that a student take either Statistics or a Geography course? Write your answer as a decimal. 0.36 O 0.24 0.54 0.45. Figure 20 shows three parts. For proper assembly, the pins must fit into the mating holes, and the bottom surfaces of parts A and B must remain in full contact with the reference surface. For 100 percent interchangeability, determine what tolerance X should be applied to the two-inch dimension. is 6. Pop statistical interchangeability is used. .495 .002 (Diam.) 500 + .002 (Diam.) 2+x- C .250 .001 (Diam.) 4.000 .003 .245 +.001 (Diam.) -2.000 1.003 B Reference surface Figure 20. Sketch of three components prior to assembly.Q4. Regression methods were used to investigate the relationship between roadway surface temperature (x) and pavement deflection (y). Summary of quantities are: Readings n = 20; Zy = 12.75; Zy? = 8.86; Ex = 1478; Ex? = 143215.8; Exy= 1083.67 1. Calculate the least square estimates of the slop and intercept. 2. Graph the regression and estimate the main statistical parameters. 3. What pavement deflection would be observed when the surface temperature is 85. 4. What is the mean pavement deflection when the surface temperature is 90.lant 5 7. Two independent random variables X and ) are given with their distribution laws X 6 P 0.2 0.3 0.5 Find 1) the variance of random variable Y. 2) the distribution law of random variable Z=0.5Y+x 2. There are 11 computers in a computer class. Special software package R is installed on eight of them. Five computers are chosen at random by visitors. Random variable X is a number of computers without package R among the chosen, Find the distribution law of X. 3. X is a continuous random variable with the cumulative distribution function X 2 Find 1) the probability density function, 2) the standard deviation of random variable X. 4. Let X be a continuous random variable with Uniform distribution in interval [-1.4;1.6]. Write its density function, find the cumulative distribution function and probability that the variable X takes value from the interval (-0.5; 2.5) 5. X is a continuous random variable with the probability density function: if x II Find the expected value of this random variable