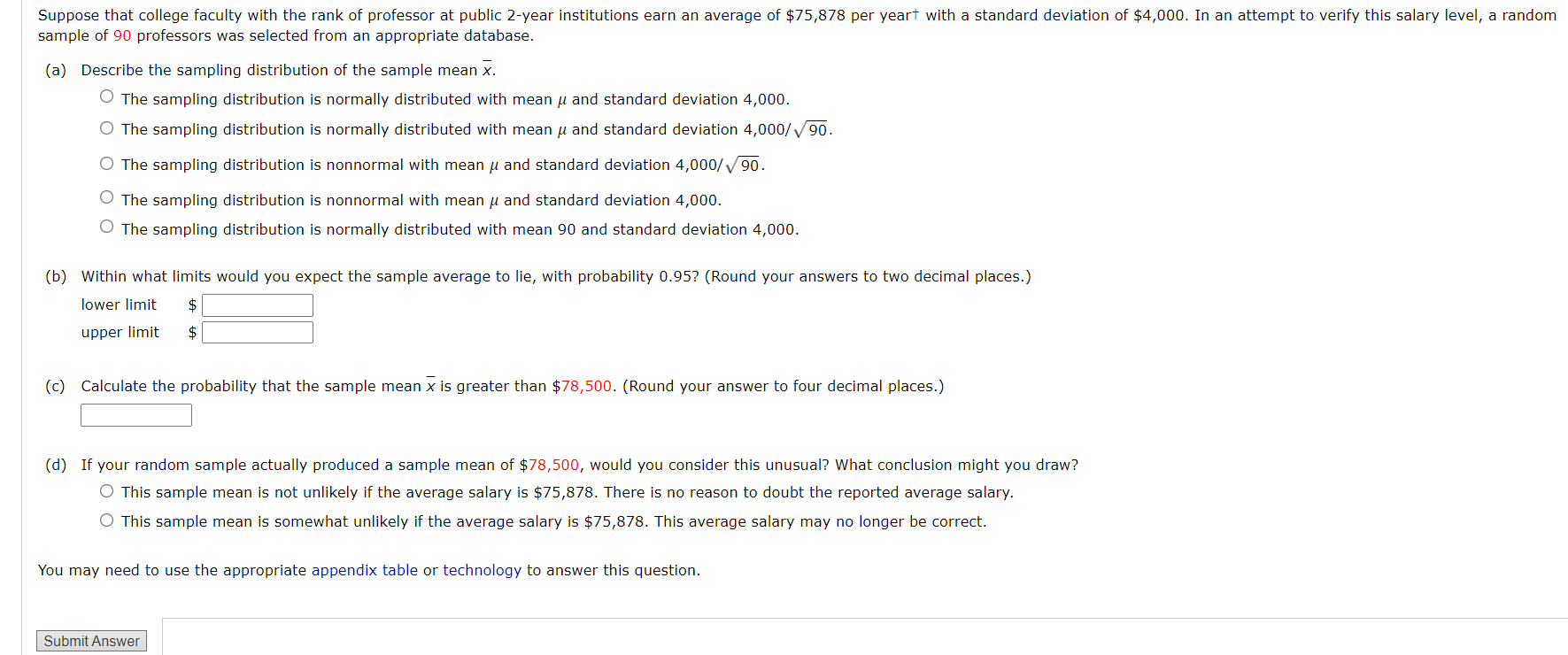
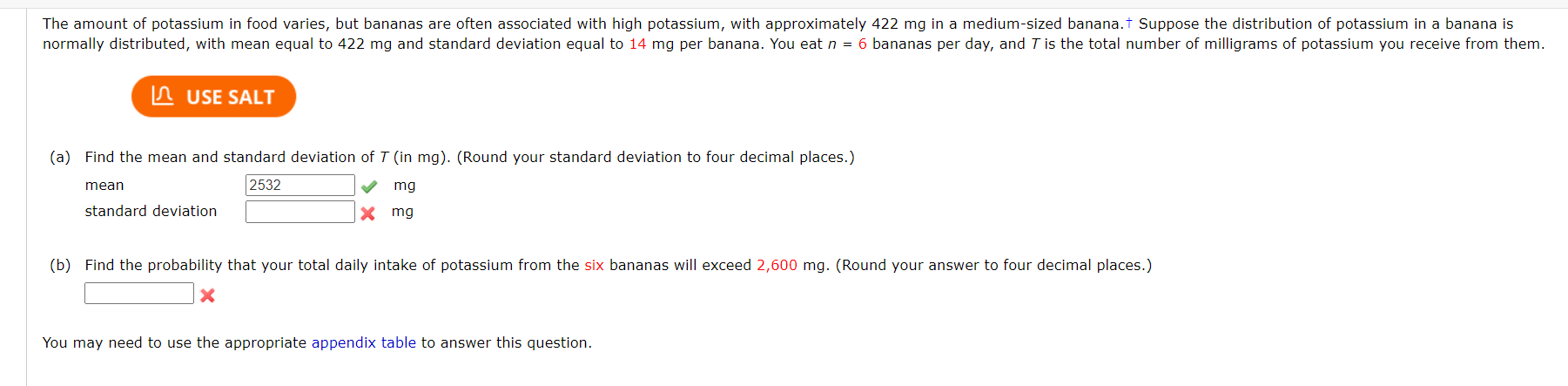
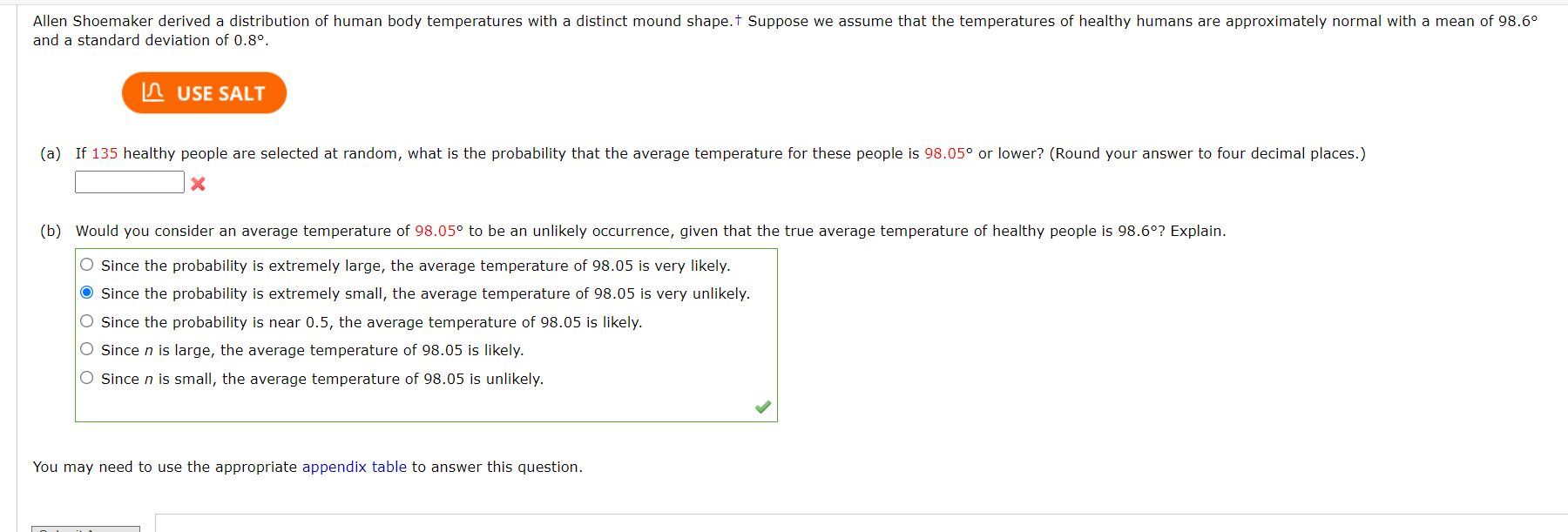
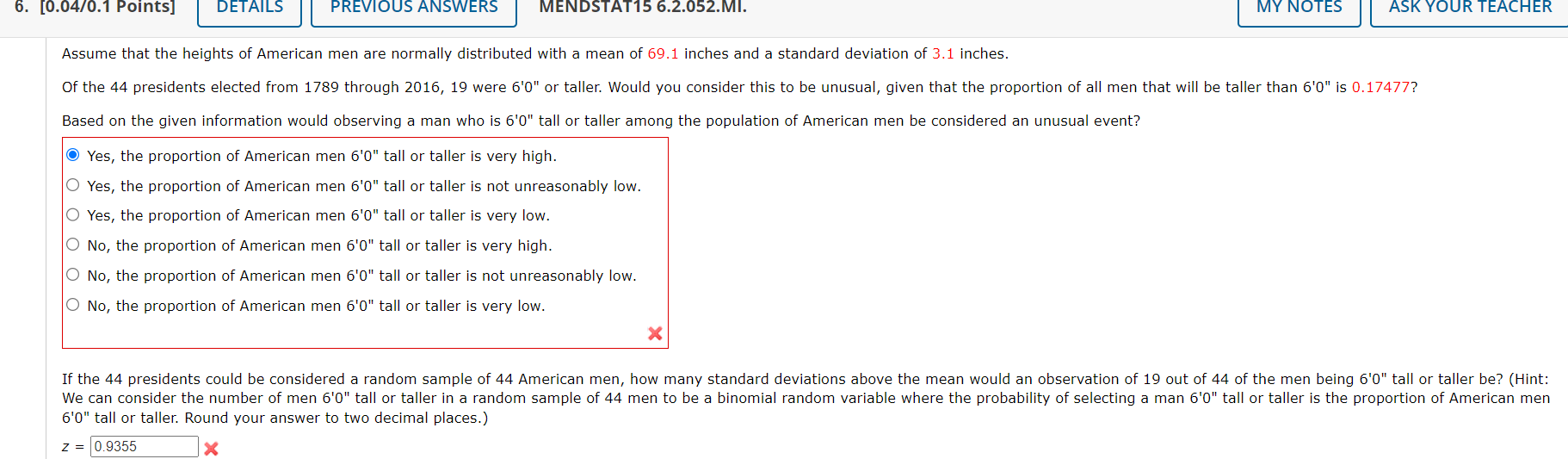
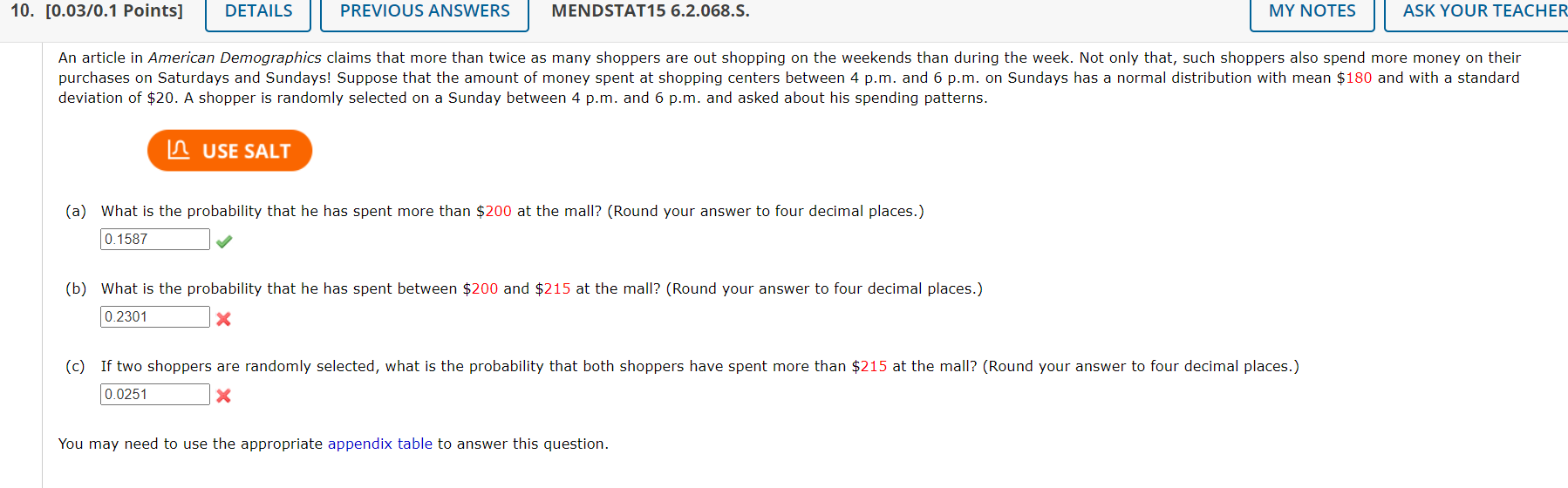
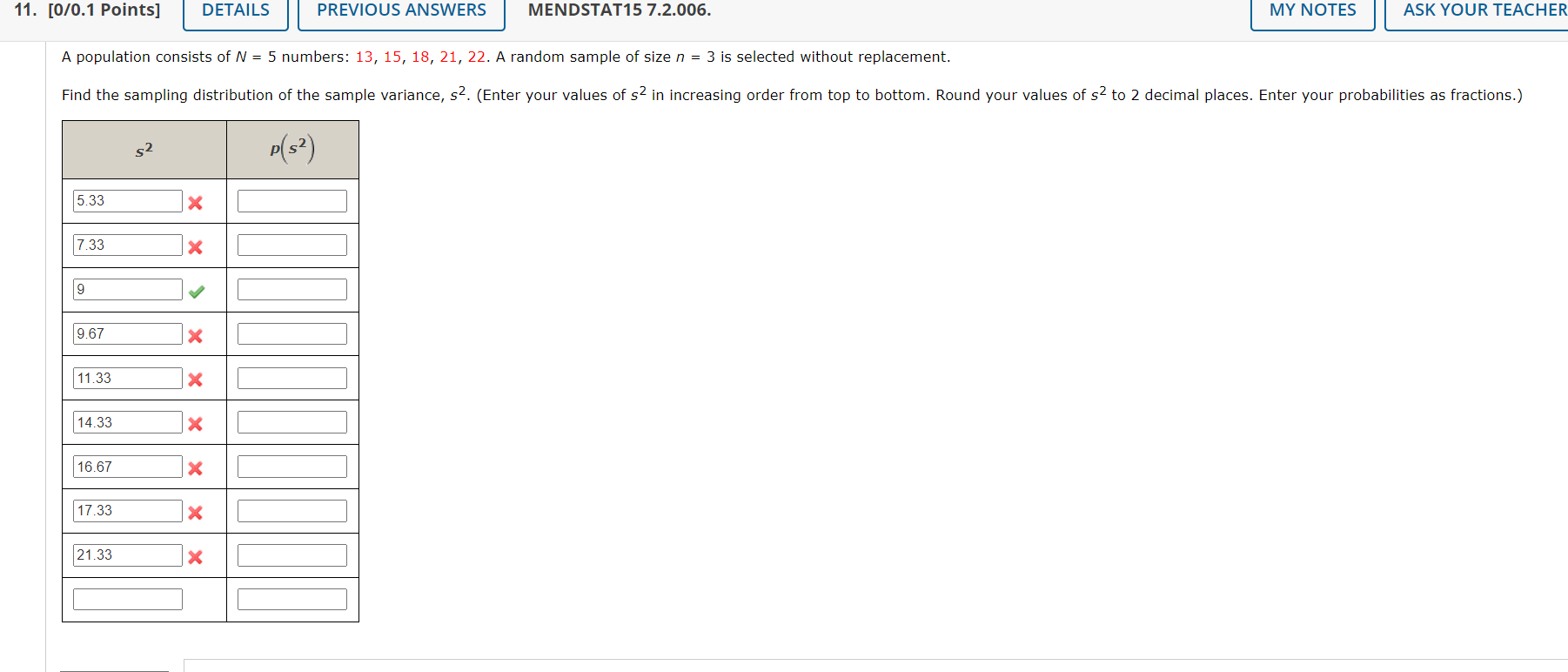
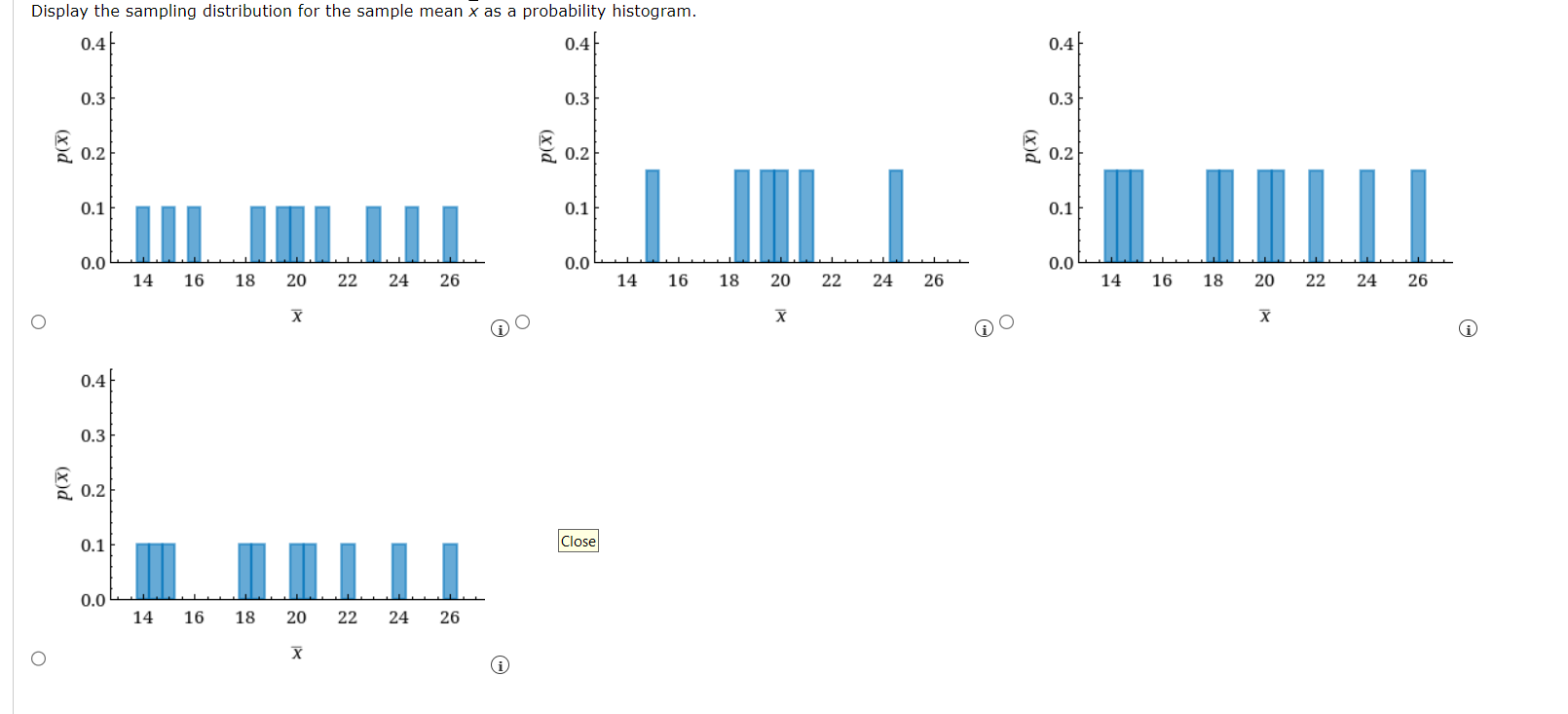
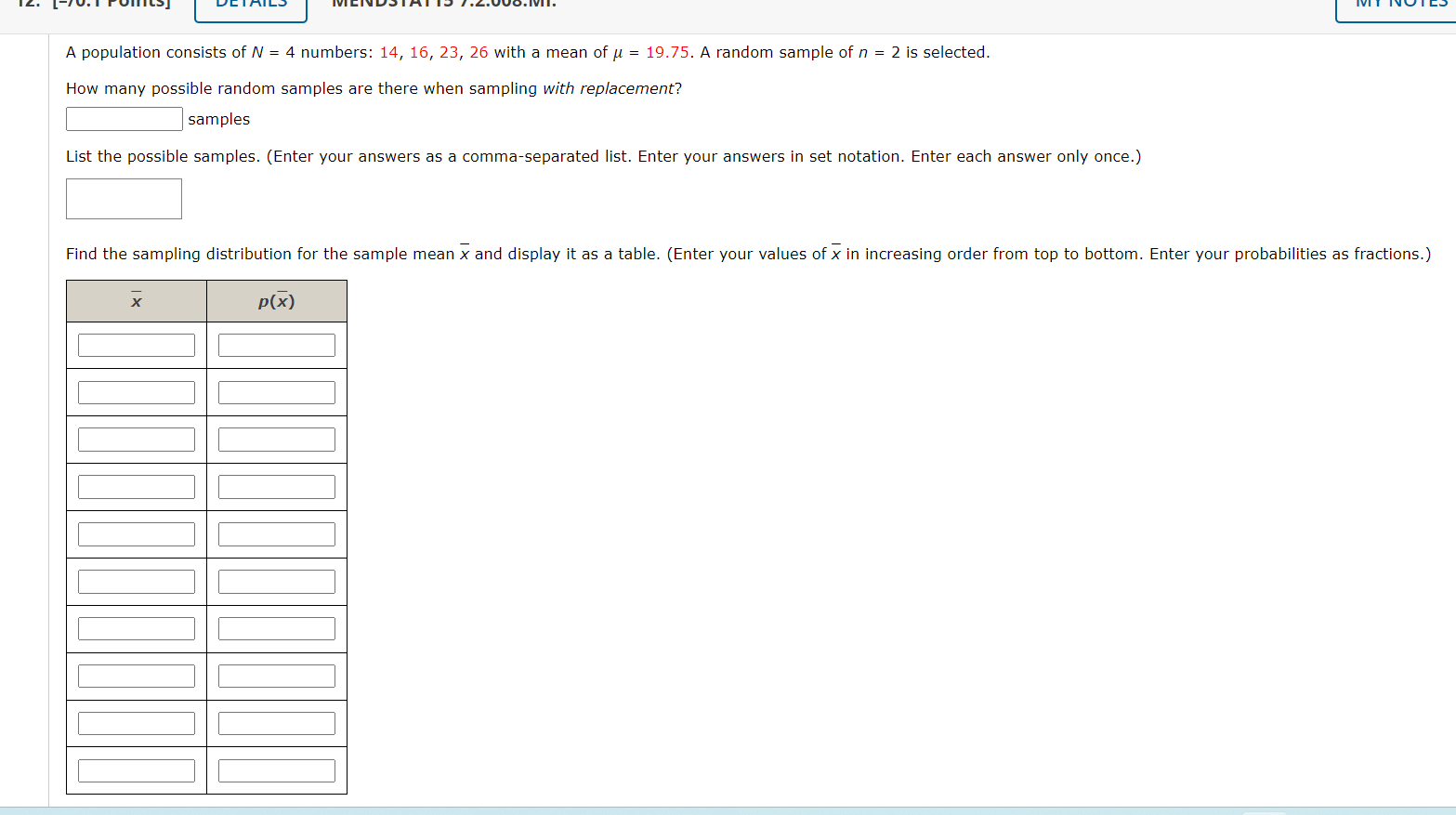
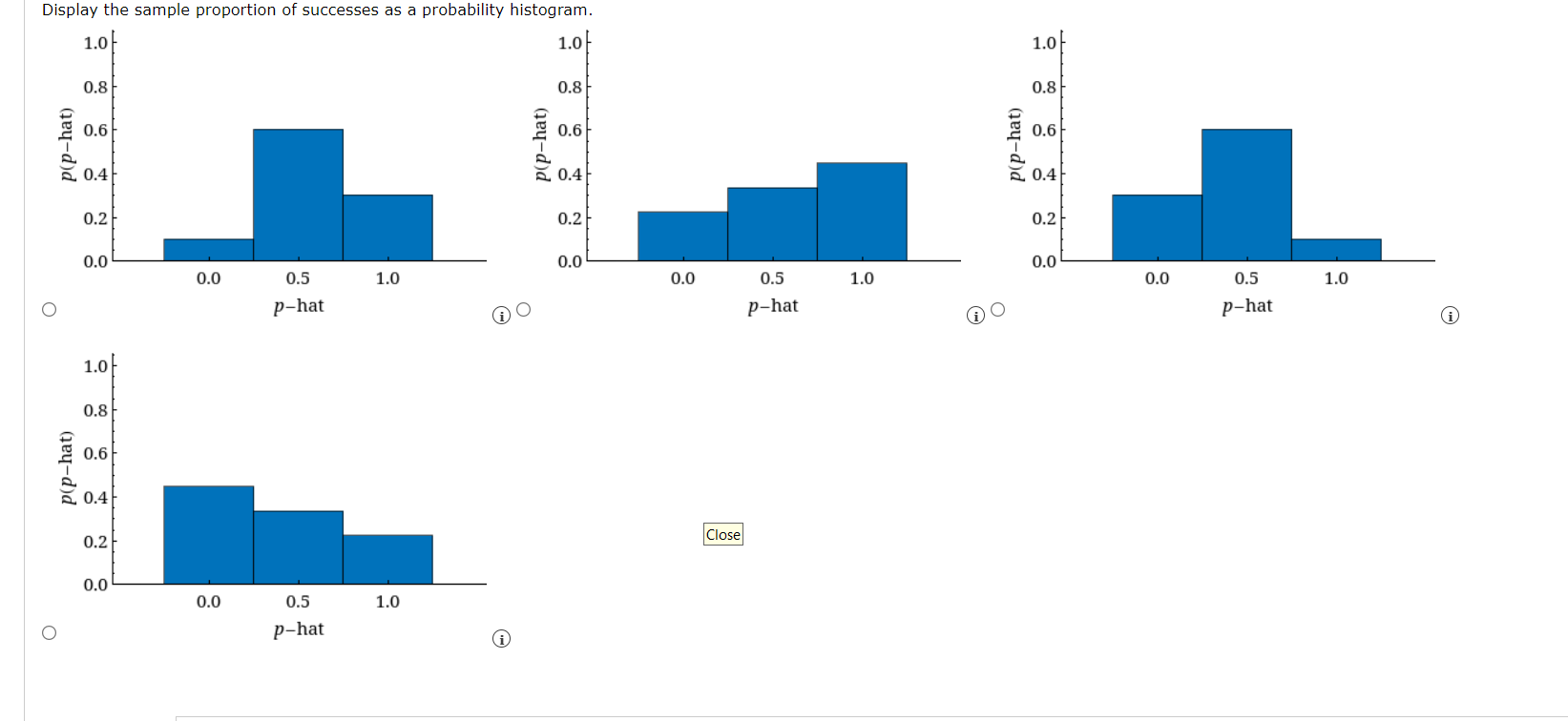
A normal random variable x has an unknown mean and standard deviation. The probability that x exceeds 4 is 0.9772, and the probability that x exceeds 6 is 0.9332. Find y and . (Round your answers to one decimal place.) PRI 71N ) P N E You may need to use the appropriate appendix table to answer this question. Need Help? Suppose that college faculty with the rank of professor at public 2-year institutions earn an average of $75,878 per yearT with a standard deviation of $4,000. In an attempt to verify this salary level, a random sample of 90 professors was selected from an appropriate database. (a) Describe the sampling distribution of the sample mean x. O The sampling distribution is normally distributed with mean u and standard deviation 4,000. O The sampling distribution is normally distributed with mean p and standard deviation 4,000/+/90. O The sampling distribution is nonnormal with mean u and standard deviation 4,000/,/90. O The sampling distribution is nonnormal with mean w and standard deviation 4,000. The sampling distribution is nermally distributed with mean 90 and standard deviation 4,000. (b) Within what limits would you expect the sample average to lie, with probability 0.95? (Round your answers to two decimal places.) ower mit [ | perimit [ ] (c) Calculate the probability that the sample mean x is greater than $78,500. (Round your answer to four decimal places.) L (d) If your random sample actually produced a sample mean of $78,500, would you consider this unusual? What conclusion might you draw? O This sample mean is not unlikely if the average salary is $75,878. There is no reason to doubt the reported average salary. This sample mean Is somewhat unlikely if the average salary is $75,878. This average salary may no longer be correct. You may need to use the appropriate appendix table or technology to answer this question. Submit Answer A paper manufacturer requires a minimum strength of 18 pounds per square inch. To check on the quality of the paper, a random sample of 13 pieces of paper is selected each hour from the previous hour's production and a strength measurement is recorded for each. Assume that the strength measurements are normally distributed with a standard deviation = 3 pounds per square inch. A USE sA (a) What is the approximate sampling distribution of the sample mean of n = 13 test pieces of paper? O The sampling distribution is nonnormal with mean u and standard deviation 3. O The sampling distribution is normally distributed with mean y and standard deviation 3/\\/'' O The sampling distribution is nonnormal with mean u and standard deviation 3/,/13. O The sampling distribution is normally distributed with mean 13 and standard deviation 3. O The sampling distribution is normally distributed with mean and standard deviation 3 (b) If the mean of the population of strength measurements is 19 pounds per square inch, what is the approximate probability that, for a random sample of n = 13 test pieces of paper, x