Question: A particle has a wave function u(x, y, z) = A z exp[b(x2 + y2 + z2)], where b is a constant. Show that this

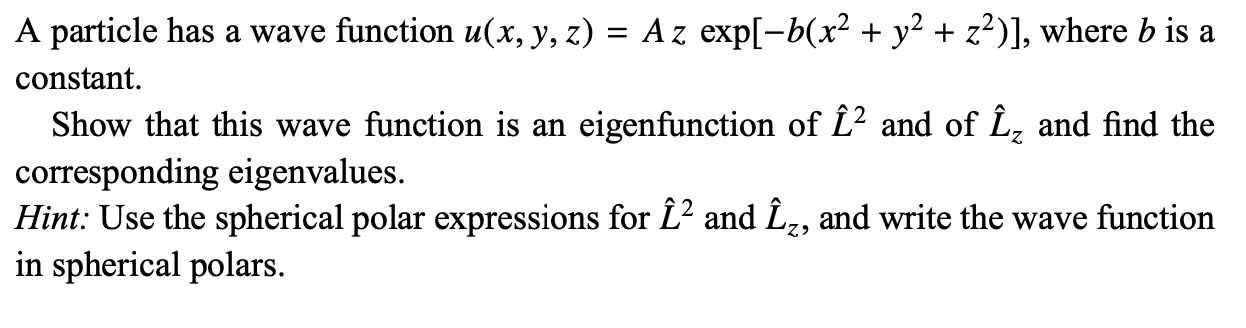
A particle has a wave function u(x, y, z) = A z exp[b(x2 + y2 + z2)], where b is a constant. Show

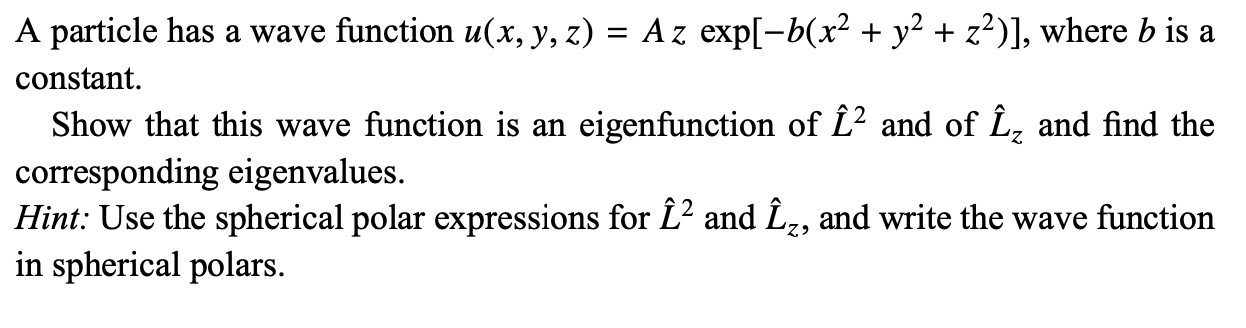
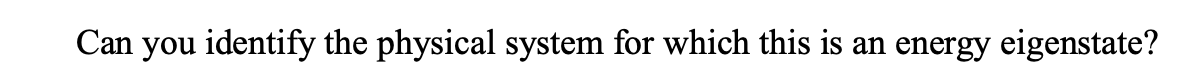
and nd the corresponding eigenvalues. Hint: Use the spherical polar expressions for

A particle has a wave function u(x, y, z) = A z exp[b(x2 + y2 + z2)], where b is a constant. Show that this wave function is an eigenfunction of 1:2 and of iz and nd the corresponding eigenvalues. Hint: Use the spherical polar expressions for Z2 and L, and write the wave function in spherical polars. Can you identify the physical system for which this is an energy eigenstate

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Questions!

HW #8 (Fault Simulation) EE 623 1. Assume you have developed an efficient table-driven event-directed logic simulation system. Consider a fan-out free circuit C having n input lines, m output line, g...

solve the answers handwritten but please type all the final answers together in the different section after solving. Thanks. 1. [-/1 Points] DETAILS SCALCET9 16.7.003. MY NOTES ASK YOUR TEACHER...

Consider the Markov Chain, Xn, on the states i = 0, 1, 2, . . . with transition matrix given by pi,i1 = p i = 1, 2, . . . pi,i+1 = 1 p i = 0, 1, . . . p0,0 = p where 0

Comparative Programming Languages.Make sense of what certified influence all of the three terms is endeavoring to show and get a handle on what all of the going with pictures suggests, inside the...

COMPLETE ALL THE QUESTIONS 1) Make a version of X.32[7] where the element type is a template argument. [10] ( 2.5) Given an Itor class like the one in X.32[8], consider how to provide iterators for...

SECTION 15.5 24. f (x, y) = sin(x - y), v= (1,1), P = (5, 6) 45. Use the geostrophi 25. f (x, y ) = tan-1 (xy), v = (1,1), P = (3,4) ern Hemisphere, winds together the isobars, 26. f (x, y ) = exy...

1 Multivariable functions and vector geometry Due date and time: Wednesday, June 7th at 9:30 AM in lecture Please ensure that you have read and understood the document \"Homework Guidelines" on the...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

10 Green's functions for PDEs In this final chapter we will apply the idea of Green's functions to PDEs, enabling us to solve the wave equation, diffusion equation and Laplace equation in unbounded...

Suppose that a 6-percent, annual-pay, Government of Canada bond that matures in two years has a yield to maturity of 6.75 percent. If inflation is expected to be 2.5 percent per year over the next...

Explain in your own words how Addison used Access to implement each of the five criteria that she and Drew developed.

7. Calculate each of the following, giving your answer in standard form, correct to 3 significant figures. (a) (2.34 x 105) x (7.12 10-4) (b) (5.1 x 10)x(2.76 10-) (c) (13.4 x 10') (4 10) 3x104 (d)...

FAST PLS In the late 1990s, the state of California deregulated many of its electricity markets, opening them up to private sector energy companies. Enron Corporation had long lobbied for...

10. What activities in your life best express the value you want others to associate with you?

7. Also complete the following sentence: This core value is important to me when I ________________________. This is the situation this core value is important to you we are looking for here.

9. What type of competence is important to have and develop in order to strengthen the core value you want others to associate with you?