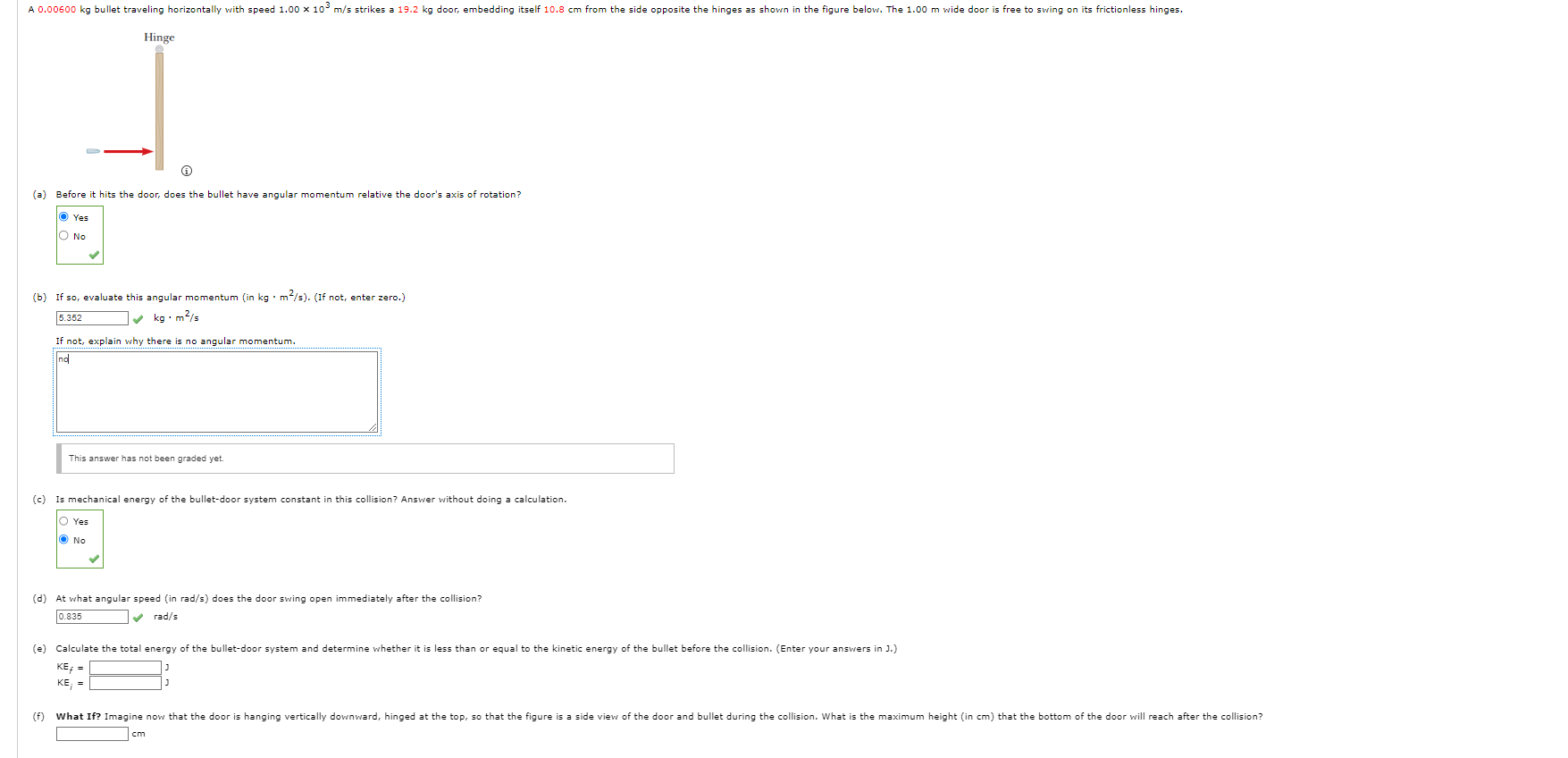
A particle is located at the position vector r = (9.001 + 10.00j) m and a force exerted on it is given by F = (8.001 + 7.00j) N. (a) What is the torque acting on the particle about the origin? -24k N . m X (b) Can there be another point about which the torque caused by this force on this particle will be in the opposite direction and half as large in magnitude? O Yes O No (c) Can there be more than one such point? Yes O No (d) Can such a point lie on the y-axis? Yes O No (e) Can more than one such point lie on the y-axis? Yes O No (f) Determine the position vector of one such point. (Give a point on the y-axis.) 3j mA wooden block of mass M resting on a frictionless, horizontal surface is attached to a rigid rod of length & and of negligible mass. The rod is pivoted at the other end. A bullet of mass m traveling parallel to the horizontal surface and perpendicular to the rod with speed v hits the block and becomes embedded in it. (a) What is the angular momentum of the bullet-block system about a vertical axis through the pivot? (Use any variable or symbol stated above as necessary.) mvl (b) What fraction of the original kinetic energy of the bullet is converted into internal energy in the system during the collision? (Use any variable or symbol stated above as necessary.) |AKI m (n + M)A 0.00600 kg bullet traveling horizontally with speed 1.00 x 10 m/s strikes a 19.2 kg door, embedding itself 10.8 cm from the side opposite the hinges as shown in the figure below. The 1.00 m wide door is free to swing on its frictionless hinges. Hinge (a) Before it hits the door, does the bullet have angular momentum relative the door's axis of rotation? O Yes O No (b) If so, evaluate this angular momentum (in kg . m /=). (If not, enter zero.) 5.352 I kg . m /s If not, explain why there is no angular momentum. This answer has not been graded yet. (c) Is mechanical energy of the bullet-door system constant in this collision? Answer without doing a calculation. Yes No (d) At what angular speed (in rad/s) does the door swing open immediately after the collision? 0.835 rad/s (e) Calculate the total energy of the bullet-door system and determine whether it is less than or equal to the kinetic energy of the bullet before the collision. (Enter your answers in J.) KE = KE; = (f) What If? Imagine now that the door is hanging vertically downward, hinged at the top, so that the figure is a side view of the door and bullet during the collision. What is the maximum height (in cm) that the bottom of the door will reach after the collision? cm