a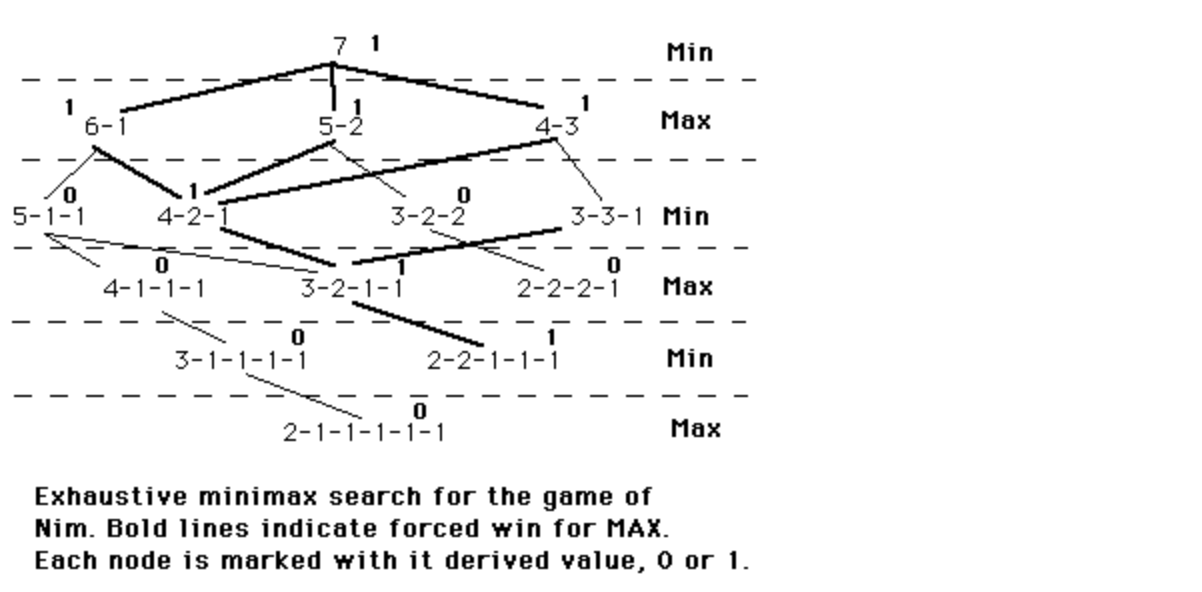
please answer question (b)(c)
(10 p) Use the minmax game strategy to play NIM. The rules for NIM are simple. Place a number of tokens between two opponents; at each move, the player whose turn comes must divide a pile of tokens into two non-empty piles of different sizes. The first player who can no longer make a move loses the game. (a) Play NIM starting with a pile of 7 (seven) tokens with the MIN player making the first move. Find the value of the game, i.e., determine the winner (MIN or MAX) for NIM when both players use the minmax strategy. Develop the whole state space for the game and show using bold face the solution path. (b) Solve the same problem as in (a), this time using the left-to-right alpha-beta pruning procedure, and show what nodes do not need to be examined. (4p) (c) Solve the same problem as in (a), this time using the right-to-left alpha-beta pruning procedure, and show what nodes would not need to be examined. (4p) Min - - - - - - - - - - -2 4-3 Max - - - - - 4-2-1 3- JI/ n 4-1-1-1 - - 3-3-1 Min ------ 0 2-2-2-1 Max 3-2-2 X 3-2-1-1 - - - - - - - - - - - - - - - - 3-1-1-1-1 2-2-1-1-1 Min - - - - - - - - - Max 2-1-1-1-1-1 Exhaustive minimax search for the game of Nim. Bold lines indicate forced win for MAX. Each node is marked with it derived value, o or 1. (10 p) Use the minmax game strategy to play NIM. The rules for NIM are simple. Place a number of tokens between two opponents; at each move, the player whose turn comes must divide a pile of tokens into two non-empty piles of different sizes. The first player who can no longer make a move loses the game. (a) Play NIM starting with a pile of 7 (seven) tokens with the MIN player making the first move. Find the value of the game, i.e., determine the winner (MIN or MAX) for NIM when both players use the minmax strategy. Develop the whole state space for the game and show using bold face the solution path. (b) Solve the same problem as in (a), this time using the left-to-right alpha-beta pruning procedure, and show what nodes do not need to be examined. (4p) (c) Solve the same problem as in (a), this time using the right-to-left alpha-beta pruning procedure, and show what nodes would not need to be examined. (4p) Min - - - - - - - - - - -2 4-3 Max - - - - - 4-2-1 3- JI/ n 4-1-1-1 - - 3-3-1 Min ------ 0 2-2-2-1 Max 3-2-2 X 3-2-1-1 - - - - - - - - - - - - - - - - 3-1-1-1-1 2-2-1-1-1 Min - - - - - - - - - Max 2-1-1-1-1-1 Exhaustive minimax search for the game of Nim. Bold lines indicate forced win for MAX. Each node is marked with it derived value, o or 1
