Question: A polynomial function of degree k is a function of the form sigma^k_i = 0 a_i middot n^i where a_0, ..., a_k are non-negative constants.

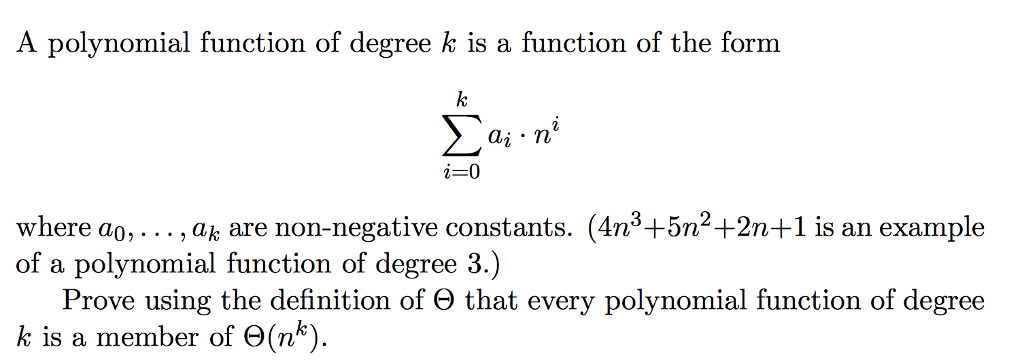
A polynomial function of degree k is a function of the

A polynomial function of degree k is a function of the form sigma^k_i = 0 a_i middot n^i where a_0, ..., a_k are non-negative constants. (4n^4 + 5n^2 + 2n + 1 is an example of a polynomial function of degree 3.) Prove using the definition of theta at every polynomial function of degree k is a member of theta(n^k)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Least Squares Approximation Hector D. Ceniceros 1 Least Squares Approximation Let f be a continuous function on [a, b]. We would like to find the best approximation to f by a polynomial of degree at...

[-/1 Points]\ SCALC9 1.2.001.\ Classify each function as a power function, root function, polynomial (state its degree), rationa\ (a) f(x)=x^(3)+8x^(2) \ power function\ root function\ polynomial...

Classify each function as a power function, root function, polynomial (state its degree), rational function, algebraic function, trigonometric function, exponential function, or logarithmic function....

If a polynomial function, f(x), has a degree greater than 4, which of the following statements true? A. The polynomial cannot be factored. B. Long division must be used to find the first factor. C....

1. Complete the sentence below. If 7 + 5i is a zero of a polynomial function of degree 5 with real coefficients, then so is If 7 + 5i is a zero of a polynomial function of degree 5 with real...

Is the function f (x) =4-7x a polynomial function? If so, state its degree and leading coefficient. O A. f(x) is not a polynomial function. O B. f(x) is a polynomial function. The degree is 7 and the...

Calculus : Please show work as organized as possible. (I get easily confused with numbers). Please put a bon on the answer to separate from the rest and put what question number it is. Thank you so...

1. Which of the following statements about a polynomial function is false? a. A polynomial function of degree n has at most n turning points. b. A polynomial function of degree n may have up to n...

oo Classify each function. (a) y = *- 8 X + 8 root function polynomial function of degree 8 trigonometric function logarithmic function rational function ero.png power function exponential function...

Maxis Sdn Bhd is a local wheel trading company and started to operate at the beginning of year 2021. Now, they are considering which inventory methods should they implemented for their company. Based...

Suppose that X1, . . . , Xn form a random sample from the normal distribution with unknown mean and known variance is 1, and the following hypotheses are to be tested: H0: = 3.5, H1: = 5.0. a....

Question 8 If prices are rising and a company is using UFO, large purchases of inventory near the end of the year wili: horeme income tases poid. forram trobone lanes paid. not change the amount of...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

The international logistics pipeline, shown in Figure 4.3, is made up of the same basic elements as any other pipeline. However, this pipeline has a number of special characteristics. Use Table 4.3...

1 Comment on Glups plans to create engineered costs from the perceived benefits of the new material-handling equipment. Glup SA supplies a range of household soaps to supermarkets in northern Europe....

What happens to the break-even point if: 2 The sales price reduces by 5 per cent? Bond SA is planning to manufacture a new product with an initial sales forecast of 3,600 units in the first year at a...