A quantum particle without Spin with mass M is limited to move inside a rectangular box of height L, which has a square base the sides of which are of length a (see illustration):

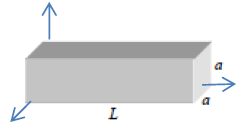
a) write out the system's Hamiltonian in Cartesian coordinates and the corresponding stationary Schroedinger equation.

b) write out the wave-functions that are eigenstates of the energy, and the corresponding eigenvalues of the energy. What is the level of degeneracy?

c) calculate the expectation value of the particle's location and its uncertainty for the ground state.

d) what needs to be the proportion between the box's height and the base's side, such that the first excited energy will be equal to the energy of the second excited level? What is the degeneracy in such a case?

e) one of the box's walls that is perpendicular to the X axis is released for it to move along the axis (the axis that does not move remains at the origin).

1) write out the eigenenergy of the eigenstates as a function of x - the distance of the box's side that is moving away from the x-axis.

2) assuming that the particle remains in the ground state throughout the entire process, calculate the force that is applied by a particle in the ground state on the box's side wall that is moving because of the change in its energy (hint: the force in a certain direction is equal to the change in energy in that same direction).

oo 1 N oo 1 N