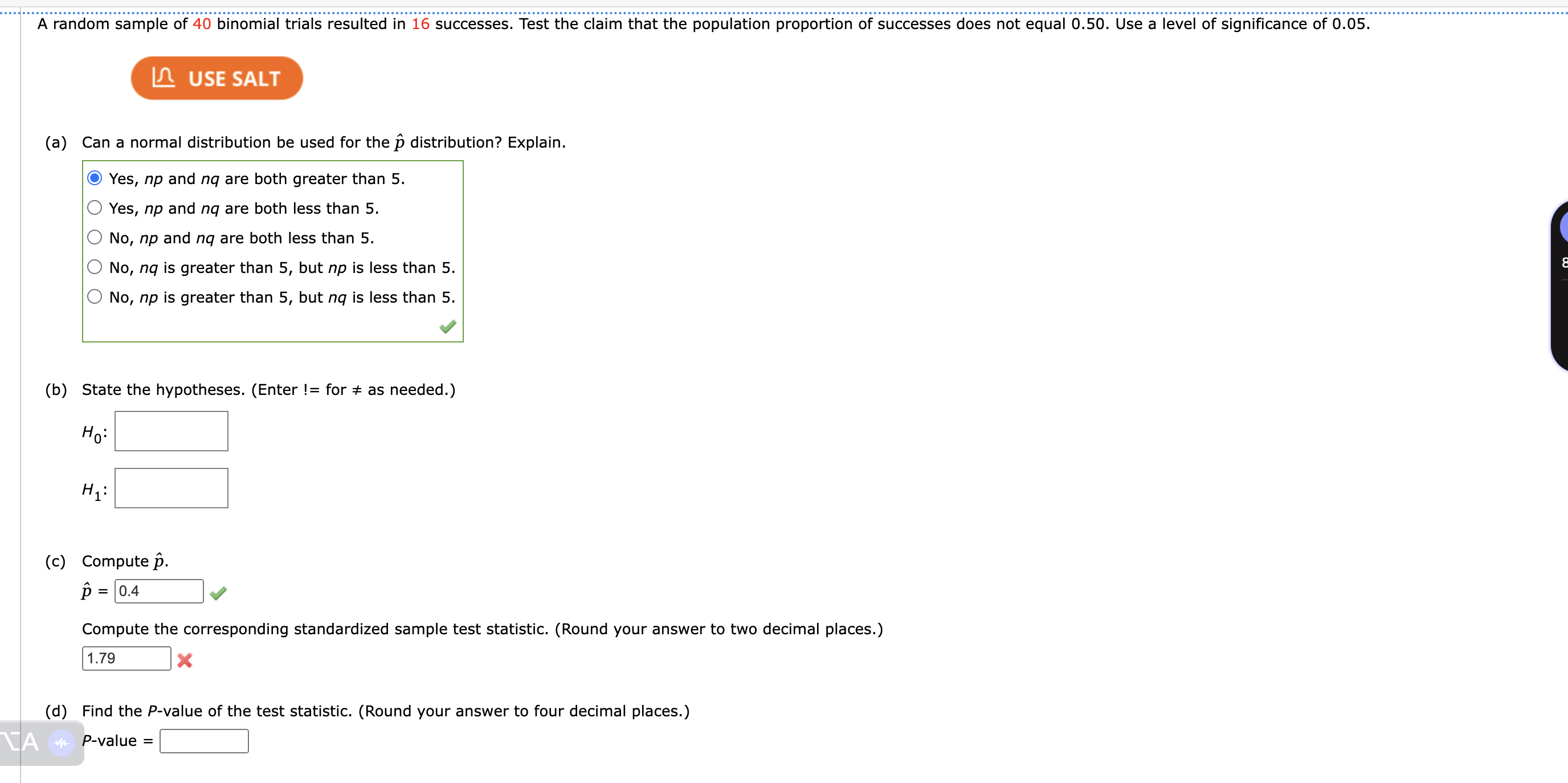
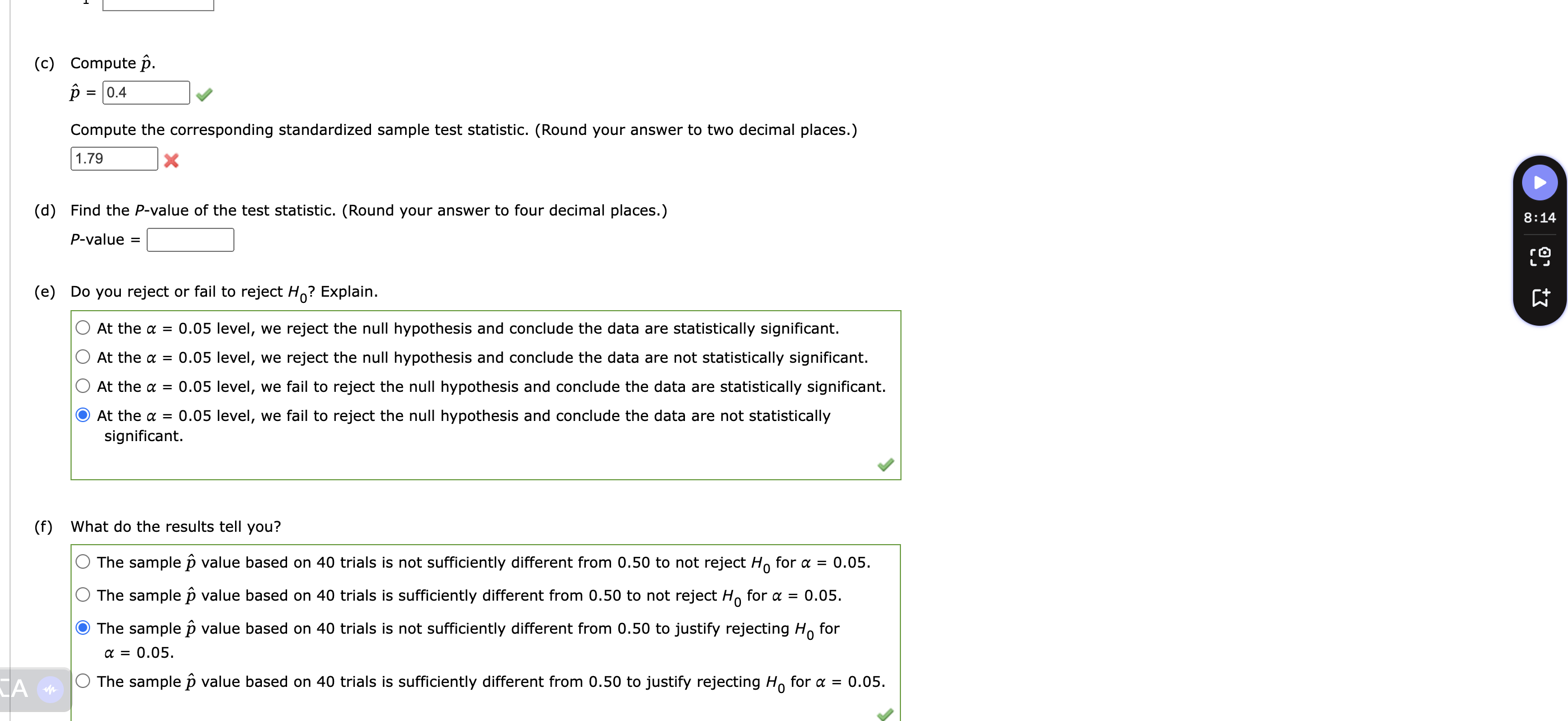
A random sample of 40 binomial trials resulted in 16 successes. Test the claim that the population proportion of successes does not equal 0.50. Use a level of significance of 0.05. USE SALT (a) Can a normal distribution be used for the p distribution? Explain. Yes, np and nq are both greater than 5. Yes, np and ng are both less than 5. No, np and nq are both less than 5. No, nq is greater than 5, but np is less than 5. No, np is greater than 5, but nq is less than 5. (b) State the hypotheses. (Enter != for # as needed.) Ho H (c) Compute p. p = = 0.4 Compute the corresponding standardized sample test statistic. (Round your answer to two decimal places.) 1.79 (d) Find the P-value of the test statistic. (Round your answer to four decimal places.) AP-value = 8 (c) Compute p. p = 0.4 Compute the corresponding standardized sample test statistic. (Round your answer to two decimal places.) 1.79 (d) Find the P-value of the test statistic. (Round your answer to four decimal places.) P-value = (e) Do you reject or fail to reject Ho? Explain. At the = 0.05 level, we reject the null hypothesis and conclude the data are statistically significant. At the = 0.05 level, we reject the null hypothesis and conclude the data are not statistically significant. At the = 0.05 level, we fail to reject the null hypothesis and conclude the data are statistically significant. At the = 0.05 level, we fail to reject the null hypothesis and conclude the data are not statistically significant. (f) What do the results tell you? 0.05. The sample p value based on 40 trials is not sufficiently different from 0.50 to not reject Ho for = The sample p value based on 40 trials is sufficiently different from 0.50 to not reject H for = 0.05. The sample p value based on 40 trials is not sufficiently different from 0.50 to justify rejecting Ho for = 0.05. The sample n value based on 40 trials is sufficiently different from 0.50 to justify rejecting H for = 0.05. 8:14