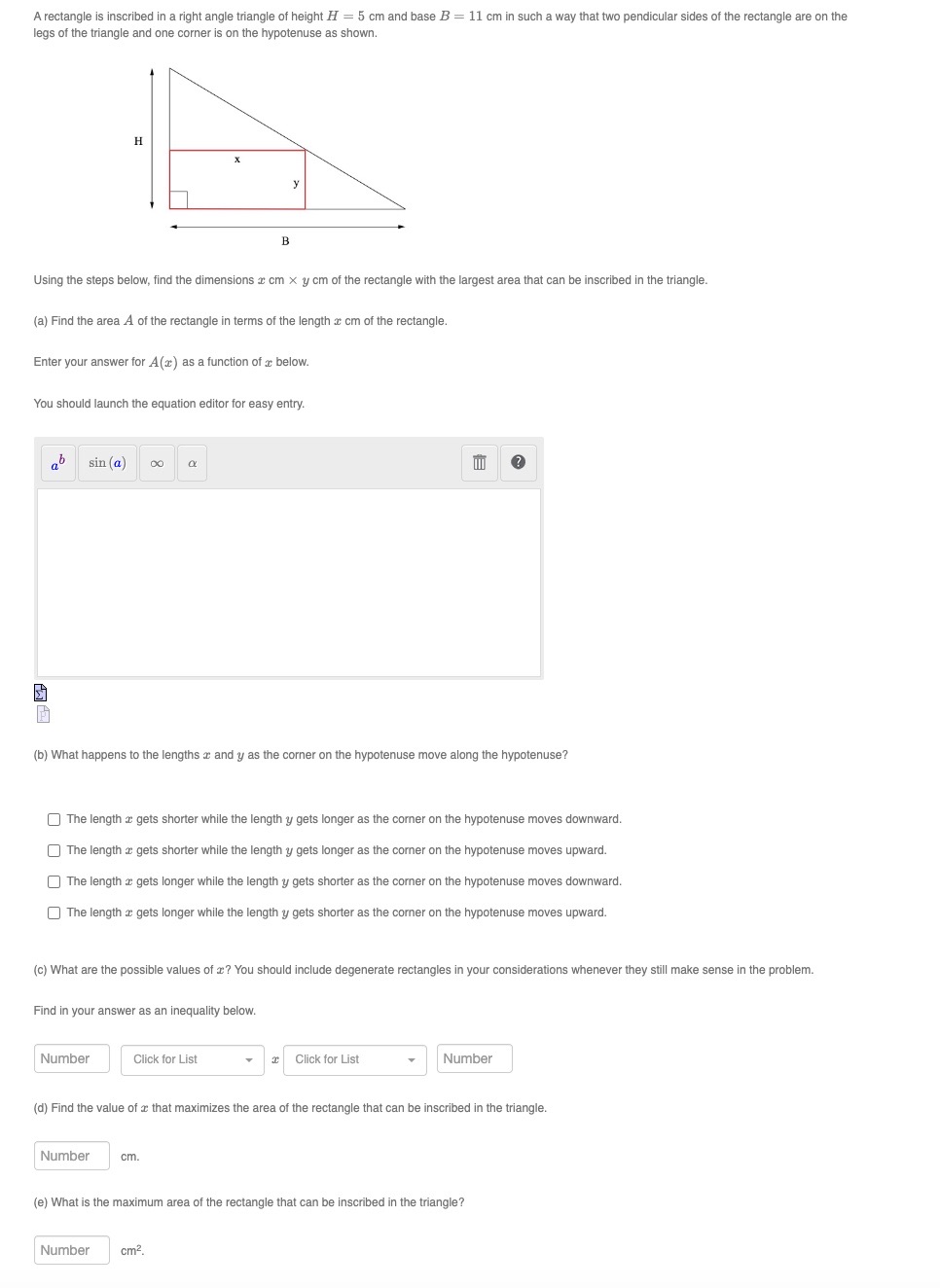
A rectangle is inscribed in a right angle triangle of height H = 5 cm and base B = 11 cm in such a way that two pendicular sides of the rectangle are on the legs of the triangle and one corner is on the hypotenuse as shown. H B Using the steps below, find the dimensions a cm x y cm of the rectangle with the largest area that can be inscribed in the triangle. (a) Find the area A of the rectangle in terms of the length & cm of the rectangle. Enter your answer for A ( ) as a function of & below. You should launch the equation editor for easy entry. sin (a) ? (b) What happens to the lengths a and y as the corner on the hypotenuse move along the hypotenuse? The length a gets shorter while the length y gets longer as the corner on the hypotenuse moves downward. The length a gets shorter while the length y gets longer as the corner on the hypotenuse moves upward. The length a gets longer while the length y gets shorter as the corner on the hypotenuse moves downward. The length a gets longer while the length y gets shorter as the corner on the hypotenuse moves upward. (c) What are the possible values of ? You should include degenerate rectangles in your considerations whenever they still make sense in the problem. Find in your answer as an inequality below. Number Click for List I Click for List Number (d) Find the value of a that maximizes the area of the rectangle that can be inscribed in the triangle. Number cm. (e) What is the maximum area of the rectangle that can be inscribed in the triangle? Number cm2