Question: A rectangular box (with no top face) can be formed by cutting four congruent squares from the corners of a rectangular sheet of cardboard and

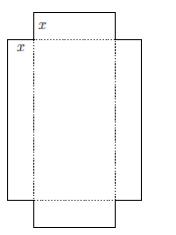
A rectangular box (with no top face) can be formed by cutting four congruent squares from the corners of a rectangular sheet of cardboard and then folding up the sides, as shown in the figure at right. The volume of the resulting box depends on the size of the cutouts. For example, suppose that the original sheet of cardboard is 5 cm by 8 cm and that the four cutouts are x cm square.

(a) Find a formula for the volume V(x) of the resulting box.

(b) What is the domain of this function? What does its graph look like?

(d) Find the maximum value of V(x).

(e) Show that the equation V(x) = 18 has only one solution.

A rectangular box (with no top face) can be formed by cutting

Step by Step Solution

★★★★★

3.26 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve this problem we need to go through each part step by step a Find a formula for the volume V... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

A rectangular box with no top and two intersecting partitions (see the figure) must hold a volume of 72 cubic inches. Find the dimensions that will require the least amount of material. Figure for 36

A shock mount constructed as shown in the figure is used to support a delicate instrument. The mount consists of an outer steel tube with inside diameter b, a central steel bar of diameter d that...

For each segment shown in the figure at right, write an equation in point-slope form for the line that contains the segment. Check your equations by graphing them on your calculator. 1

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

270 Chapter 4 Applications of Derivatives c. What is the largest area the rectangle can have, and what are its dimensions? 12. Find the volume of the largest right circular cone that can be in- X...

Reference: Calculus and Its Applications, 12th, by Marvin L. Bittinger and David Ellenbogen Book Elementary Applied Calculus I need help with questions These are practice questions Links to Book...

[1 point) A box with no top is to be built by taking a sheet of cardboard measuring 13inches by 23inches, cutting zinch squares out of each comer, and folding up the sides. a} What are the length and...

I know these are a lot of questions. So if you can only do some of them that's okay. Thank you so very much in advance for your help. Find the dimensions and volume of the right circular cylinder of...

9/14/10 12:27 PM Page 321 Chapter dug84356_ch05a.qxd 5 Factoring The sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. Today,...

having trouble with question 1 2 b. and 3b On February 1 2018. Arrow Construction Company entered into a three-year construction contract to build a bridge for a price of $8,000,000. During 2018,...

The S-N-curve for an elastic material is characterized by the Basquin relationship, = C.N where C is a material constant, is the stress amplitude, Nr is the number of fully-reversed- stress cycles to...

2. Write a clarifying statement for your top five prioritized values. Answer the question, "What does this value really mean to me?" If you were living that value perfectly, what would your behaviour...

When a failure-to-extract malfunction is experienced in the AR platform, the barrel must be removed in order to properly replace the extractor

X; as an estimate of the population mean Problem 7. (10 POINTS) WEIGHTED SAMPLE MEAN In lectures, we discussed the sample mean X = =i. Let us consider a more general class of estimators: n X = wiXi,...

a ) Simplify this distributed load to an equivalent load / s . b ) Solve the reactions at A and B . and draw FBD of equivalent loading? 6 kN/m 9 kN/m 00 1.5 m 2 m 3.5 m

operating activities? 7. In determining the cash flow from operating activities using the indirect method, why is it necessary to add depreciation back to net income? Give an example of another item...

Carlton Stokes owns and operates a car-detailing business named SuperShine & Detailing. For $150, Carltons business will hand wash and wax customers cars, vacuum the interior, and thoroughly clean...

Using the data of Problem 6.27, determine the velocity head of the fluid leaving the impeller. What pressure rise would result from such a velocity head? Data From Problem 6.27 Water flows through...

Spherical polymer beads of 3.0 mm (0.3 cm) diameter contain residual solvent from the polymer-casting process. Initially, the bead contains 0.20 wt% of residual solvent uniformly distributed within...

A flat silicon wafer 15 cm in diameter (surface area 176.7 cm 2 ) is removed from an annealing furnace and laid flat-side down onto a flat insulating surface. It is then allowed to cool down to room...

Remodeling an office will cost $ 25,000 and will generate savings of $ 3,000 the first year, $ 4,000 the second year, and $ 5,000 per year thereafter. How long will it take to recoup the initial cost...

Given the following diagram, a. What is the capacity of this system? b. If the capacity of one operation could be increased in order to increase the output of the system, which operation should it...

A small building contractor has recently experienced two successive years in which work opportunities exceeded the firms capacity. The contractor must now make a decision on capacity for next year....