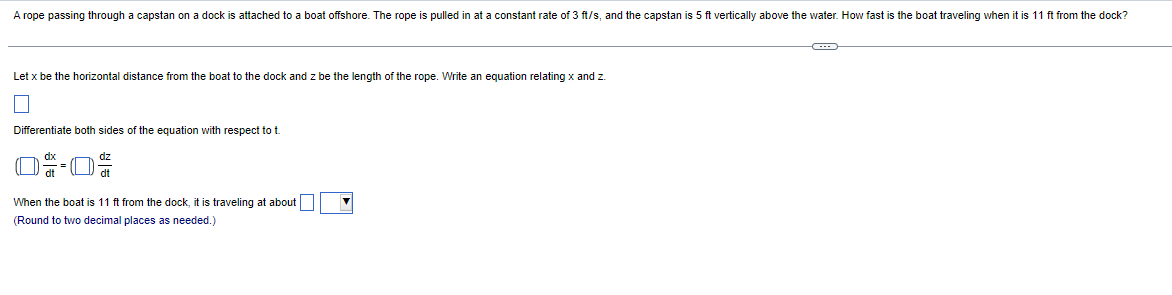
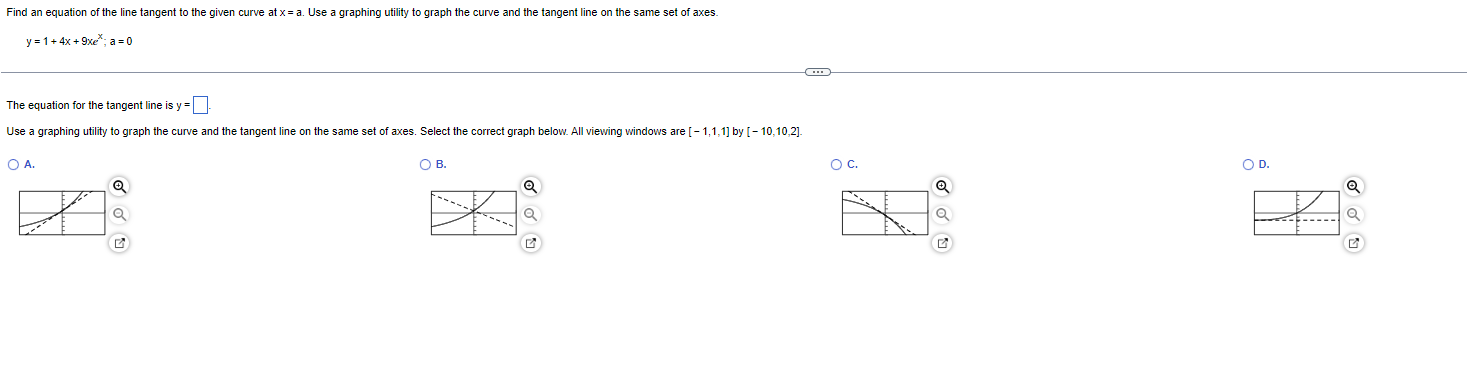
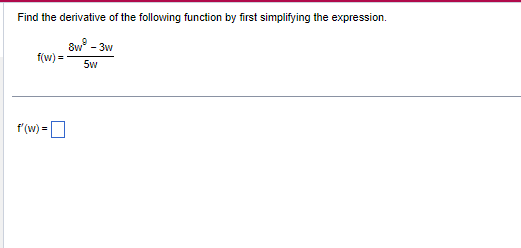
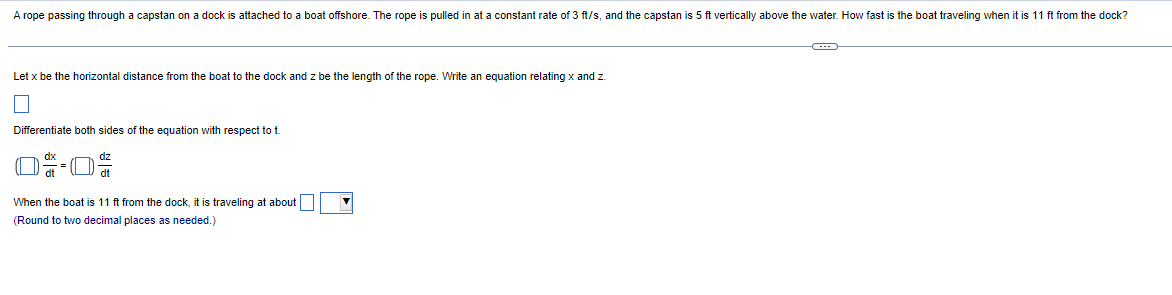
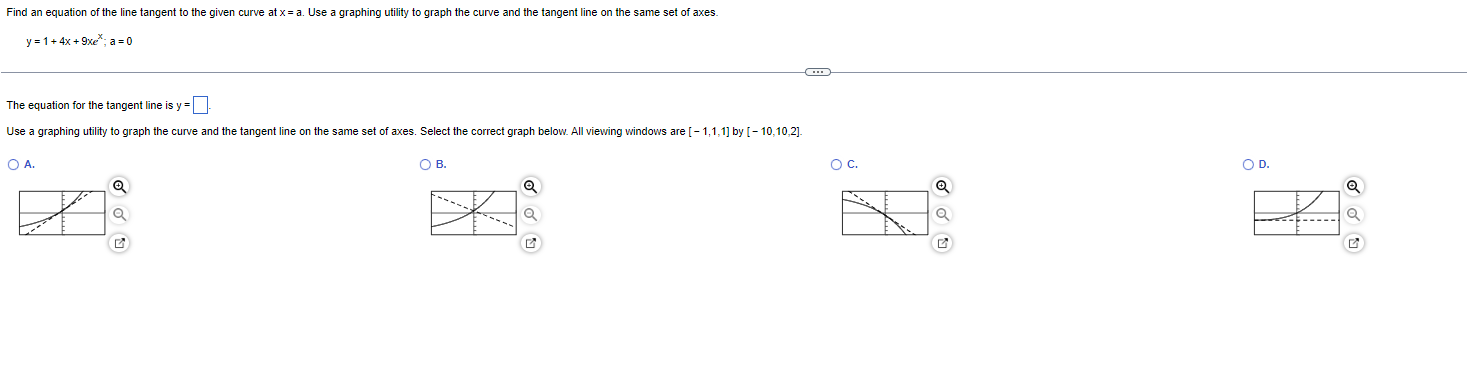
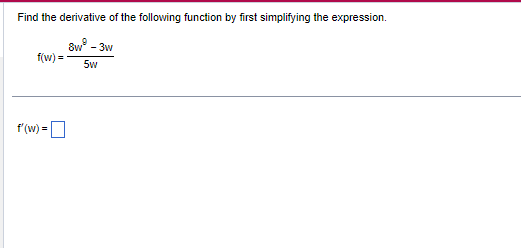
A rope passing through a capstan on a dock is attached to a boat offshore. The rope is pulled in at a constant rate of 3 ft/s, and the capstan is 5 ft vertically above the water. How fast is the boat traveling when it is 11 ft from the dock? Let x be the horizontal distance from the boat to the dock and z be the length of the rope. Write an equation relating x and z. Differentiate both sides of the equation with respect to t. dt When the boat is 11 ft from the dock, it is traveling at about( V (Round to two decimal places as needed.)Find an equation of the line tangent to the given curve at x = a. Use a graphing utility to graph the curve and the tangent line on the same set of axes. y = 1+4x + 9xe ; a=0 The equation for the tangent line is y =] Use a graphing utility to graph the curve and the tangent line on the same set of axes. Select the correct graph below. All viewing windows are [ - 1, 1, 1] by [ - 10,10,2]- O A. O B. O C. OD. aFind the derivative of the following function by first simplifying the expression. Bw - 3w f(w) = 5w f (w) =Question 1 : The equation relating X and z is x"2 + 5A2 = z"2. Differentiating the above w.r.t. time t, x dx/dt = z dz/dt. When the boat is 11 ft. from the dock, it is traveling at about 3.3 ft/seo. Question 2: The equation for the tangent line is y = i3x+1. The correct option is (A). Question 3 : f'(w) = (64/5)w"7