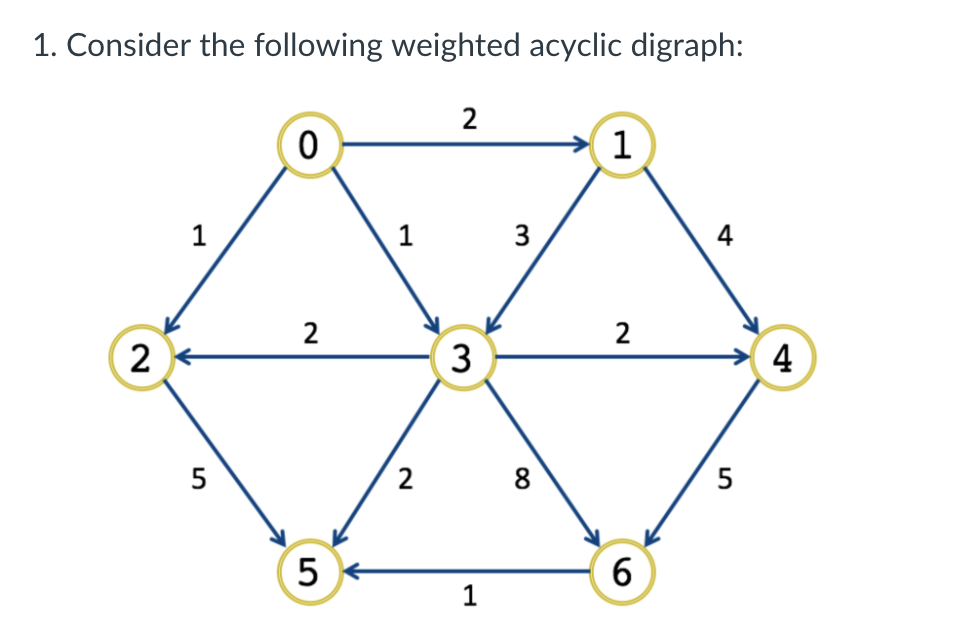
a. Show how this graph is represented as an adjacency matrix.

b. Show how this graph is represented as adjacency lists.

c. You run the memoized Shortest Path algorithm (listed below) to find (4, 2), which is the length of the shortest path from vertex 4 to vertex 2. Along the way, you update the cache. Recall that the cache is a table where each entry contains a vertex x and (4, x). Show the state of the cache when the algorithm terminates.

d. Why does the algorithm not work for graphs with cycles?

Map cache = new HashMap();

int shortestPath(int s, int t) {

if (cache.containsKey(t))

return cache.get(t);

int ans = 0;

if (s != t) {

ans = Integer.MAX_VALUE;

for (int x : in(t))

ans = Math.min(ans, shortestPath(s, x) + weight(x, t));

}

cache.put(t, ans);

return ans;

}

1. Consider the following weighted acyclic digraph: 1 1 1 4 2 3 1 1. Consider the following weighted acyclic digraph: 1 1 1 4 2 3 1