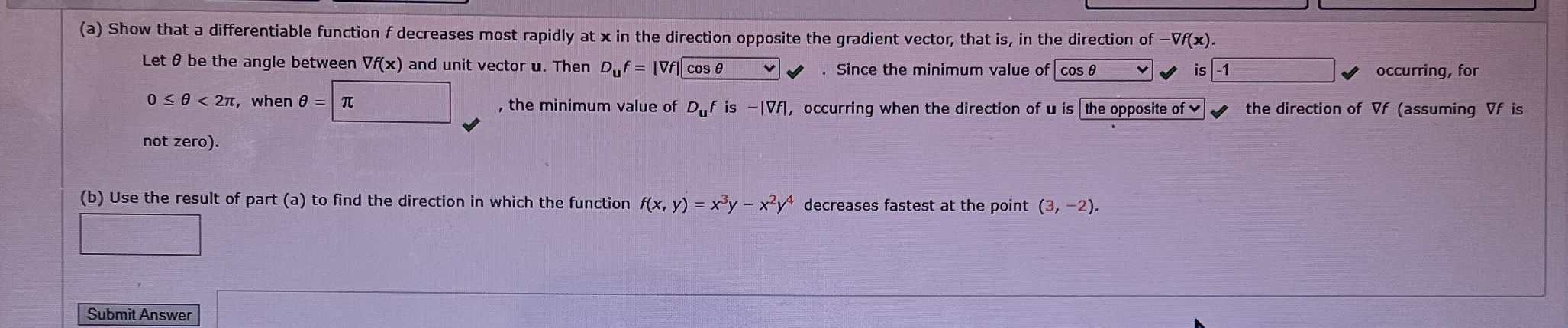
$($a$)$ Show that a differentiable function $f$ decreases most rapidly at $x$ in the direction opposite the gradient vector, that is$,$ in the direction of $-$gradf$(x).$

Let $$ be the angle between gradf$(x)$ and unit vector $u.$ Then $D_{u}f=|gradf|.$ Since the minimum value of $$ is $$ occurring, for when $=,$ the minimum value of $D_{u}f$ is $-|gradf|,$ occurring when the direction of $u$ is $$ the direction of gradf $($assuming gradf is not zero$).$

$($b$)$ Use the result of part $($a$)$ to find the direction in which the function $f(x,y)=x^{3}y-x^2{y}^4$ decreases fastest at the point $(3,-2).$