Question: (a) Show that (f(x1)f(X2))(g(x1)- 8(X2)) is a non-negative random variable. (b) Now suppose that X1 andX2 are independent and equi-distributed. Show that 2Cov(f(x1), 8(X1))

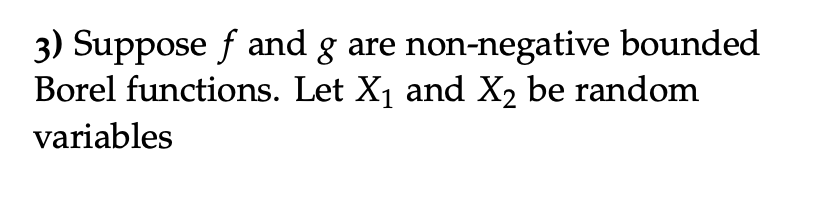
(a) Show that (f(x1)f(X2))(g(x1)- 8(X2)) is a non-negative random variable. (b) Now suppose that X1 andX2 are independent and equi-distributed. Show that 2Cov(f(x1), 8(X1))

(a) Show that (f(x1)f(X2))(g(x1)- 8(X2)) is a non-negative random variable. (b) Now suppose that X1 andX2 are independent and equi-distributed. Show that 2Cov(f(x1), 8(X1)) - = Cov(f(x1)- f(x2),g(X1) g(X2)). (c) Show that Cov(f(x1), 8(X1)) 0. 3) Suppose and g are non-negative bounded Borel functions. Let X and X2 be random variables

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let Ln be the red-black tree with the integers 1, 2,..., n inserted one at a time from lowest to highest, but rebalancing following the three cases. (a) [10 marks] Neatly draw the resulting trees...

If det A = 2, det B = -1, and det C = 3, find: (a) (b) det X B 0 (d) det 0 B 0

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

X UG f M M C S a G + V X C online.mun.ca/d21/le/content/485955/viewContent/4518693/View * Homework Assignment #6 Questions 1. For each of the following, test for the significance of the difference in...

Suppose f and g are non-negative bounded Borel functions. Let X1 and X2 be random variables A. Show that ( f (X1) f (X2))(g(X1) g(X2)) is a non-negative random variable. B. Now suppose that X1 andX2...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Planning Demand and Supply in a Supply Chain Capacity Planning and Assignment 1 utdallas.edu/~metin Outline Capacity Planning Product-to-plant Assignment utdallas.edu/~metin 2 Deterministic Capacity...

The new line character is utilized solely as the last person in each message. On association with the server, a client can possibly (I) question the situation with a client by sending the client's...

The scope of history is wide-the theme is the past, present, and future of man in the light of this statement, discuss the scope of the subject.

The following note related to stockholders equity was reported in Wiebold, Inc.s annual report. On February 1, the Board of Directors declared a 3-for-2 stock split, distributed on February 22 to...

Mary is 3 8 years old and many of her friends have gotten into trouble using their credit cards to buy things they can't afford. She feels lucky that her grandmother told her that credit is dangerous...

Find the z-score (the number of standard deviations from the mean) for the following measurements. 1. A value of 11.0 drawn from a normal distribution with mean 13.0 and standard deviation 1.2. 2. A,...

Corn Company incurs a cost of $35 per unit, of which $20 is variable, to make a product that normally sells for $58. A foreign wholesaler offers to buy 6,000 units at $31 each. Corn will incur...

Find the value of z if the area under a standard normal curve (a) To the right, of z is 0.3622; (b) To the left of a is 0.1131; (c) Between 0 and z, with z > 0, is 0.4838; (d) Between z and z, with z...

Mann Company incurs a cost of $35 per unit, of which $20 is variable, to make a product that normally sells for $58. A foreign wholesaler offers to buy 6,000 units at $31 each. Mann will incur...

Mr. Lion, who is in the 39.6 percent tax bracket, is the sole shareholder of Toto, which manufactures greeting cards. Totos average annual net profit (before deduction of Mr. Lions salary) is...

Design a minimum-mass symmetric three-bar truss (the area of member 1 and that of member 3 are the same) to support a load P, as was shown in Fig. 2.9. The following notation may be used: Pu = P cos...

The equation of state of a gas is given by the Berthelot equation (P+a/Tv)(-b)=RT. (a) Find values of the critical temperature Te, the critical molar volume vc, and the critical pressure Pc, in terms...

A boy blows a soap bubble of radius R which floats in the air a few moments before breaking. What is the difference in pressure between the air inside the bubble and the air outside the bubble when...

A liquid crystal is composed of molecules which are elongated (and often have flat segments). It behaves like a liquid because the locations of the center of mass of the molecules have no long-range...