A.) show that the following algorithm does not correctly solve this problem, by giving an instance on which it does not return the correct answer

B.) Give an efficient algorithm that takes values for l1, l2,...,ln and h1, h2, hn and returns the value of an optimal plan

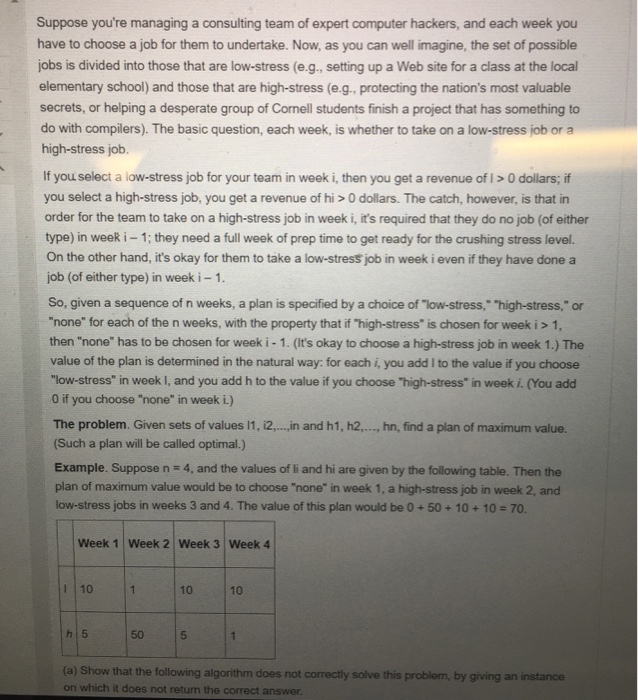
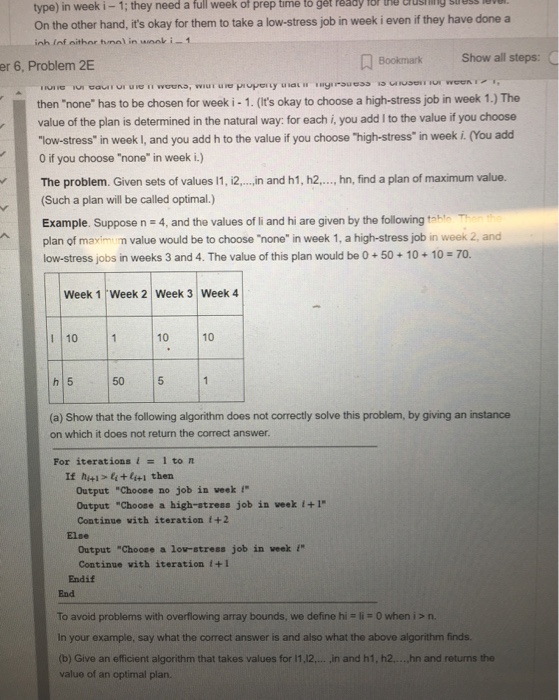
Suppose you're managing a consulting team of expert computer hackers, and each week you have to choose a job for them to undertake. Now, as you can well imagine, the set of possible jobs is divided into those that are low-stress (e.g., setting up a Web site for a class at the local elementary school) and those that are high-stress (e.g., protecting the nation's most valuable secrets, or helping a desperate group of Cornell students finish a project that has something to do with compilers). The basic question, each week, is whether to take on a low-stress job or a high-stress job. If you select a low-stress job for your team in week i, then you get a revenue of I > 0 dollars; if you select a high-stress job, you get a revenue of hi > 0 dollars. The catch, however, is that in order for the team to take on a high-stress job in week i, it's required that they do no job (of either type) in week i-1; they need a full week of prep time to get ready for the crushing stress level. On the other hand, it's okay for them to take a low-stress job in week i even if they have done a job (of either type) in week i 1 So, given a sequence of n weeks, a plan is specified by a choice of low-stress," "high-stress," o "none" for each of the n weeks, with the property that if high-stress is chosen for week i > 1, then "none" has to be chosen for week i - 1. (It's okay to choose a high-stress job in week 1.) The value of the plan is determined in the natural way: for each i, you add I to the value if you choose "low-stress" in week I, and you add h to the value if you choose "high-stress" in week i. (You add 0 if you choose "none" in week i.) The problem. Given sets of values 11, i2.,., .in and h1, h2,.., hn, find a plan of maximum value. (Such a plan will be called optimal.) Example. Suppose n 4, and the values of li and hi are given by the following table. Then the plan of maximum value would be to choose "none" in week 1, a high-stress job in week 2, and low-stress jobs in weeks 3 and 4. The value of this plan would be O+50+ 10+10-70. Week 1 Week 2 Week 3 Week 4 1 |10 10 10 50 5 (a) Show that the following algorithm does not correctly solve this on which it does not return the correct answer problem, by giving an instance