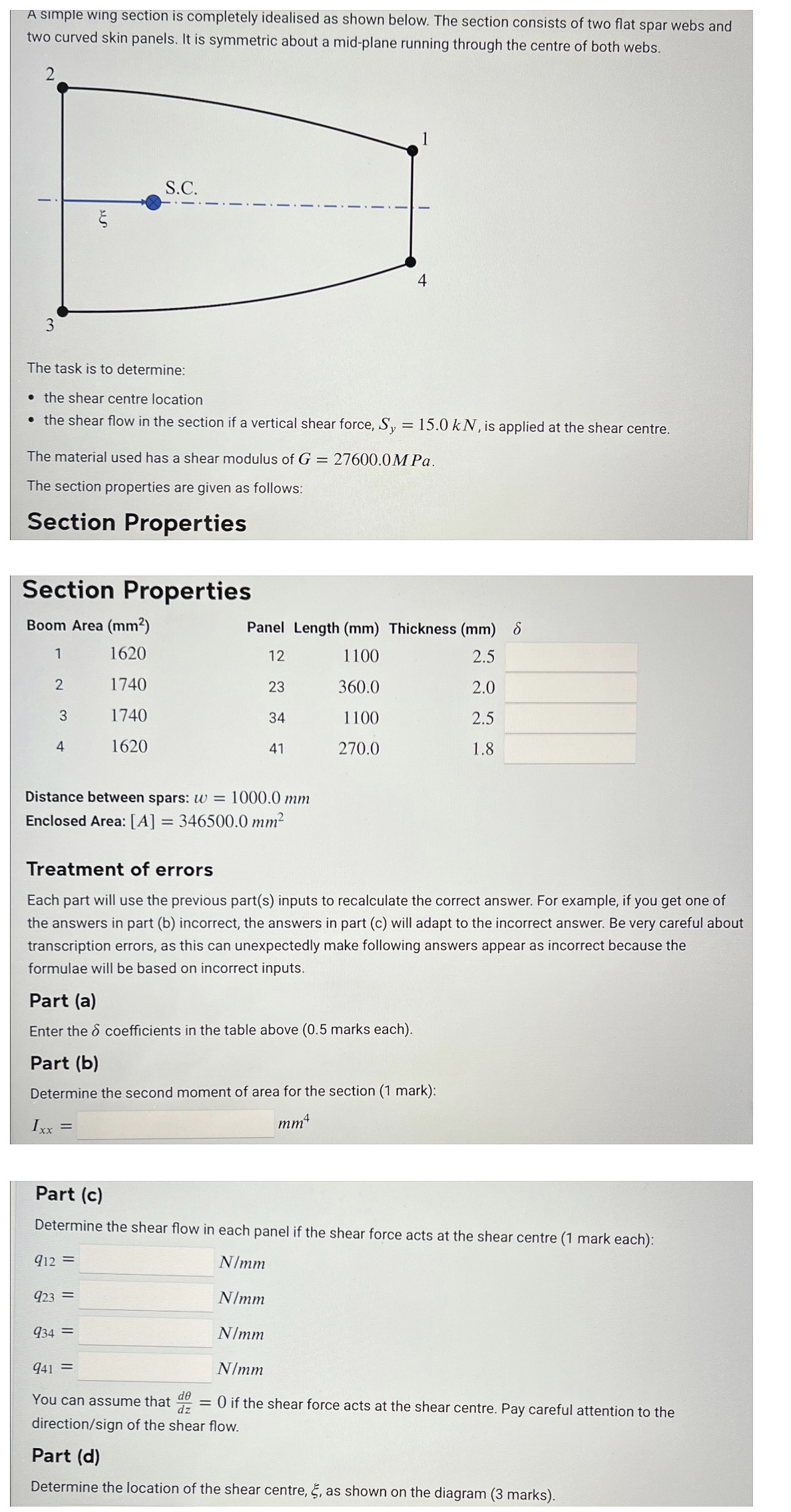
A simple wing section is completely idealised as shown below. The section consists of two flat spar webs and two curved skin panels. It is symmetric about a mid-plane running through the centre of both webs. 2 S.C. 4 3 The task is to determine: the shear centre location the shear flow in the section if a vertical shear force, Sy = 15.0 kN, is applied at the shear centre. The material used has a shear modulus of G = 27600.0MPa. The section properties are given as follows: Section Properties Section Properties Boom Area (mm) Panel Length (mm) Thickness (mm) 8 1 1620 12 1100 2.5 2 1740 23 360.0 2.0 3 1740 34 1100 2.5 4 1620 41 270.0 1.8 Distance between spars: w = 1000.0 mm Enclosed Area: [A] = 346500.0 mm Treatment of errors Each part will use the previous part(s) inputs to recalculate the correct answer. For example, if you get one of the answers in part (b) incorrect, the answers in part (c) will adapt to the incorrect answer. Be very careful about transcription errors, as this can unexpectedly make following answers appear as incorrect because the formulae will be based on incorrect inputs. Part (a) Enter the coefficients in the table above (0.5 marks each). Part (b) Determine the second moment of area for the section (1 mark): Ixx = mm4 Part (c) Determine the shear flow in each panel if the shear force acts at the shear centre (1 mark each): 912= 923= 934= 941= N/mm N/mm N/mm N/mm de dz You can assume that = 0 if the shear force acts at the shear centre. Pay careful attention to the direction/sign of the shear flow. Part (d) Determine the location of the shear centre, , as shown on the diagram (3 marks). Part (d) Determine the location of the shear centre, 5, as shown on the diagram (3 marks). $ = mm Hint: A convenient place to take the torque equilibrium origin is the intersection of the symmetry plane with panel 23. The area subtended by panels 12 and 34 is then equal. The total cell area can then be manipulated to find the subtended areas.