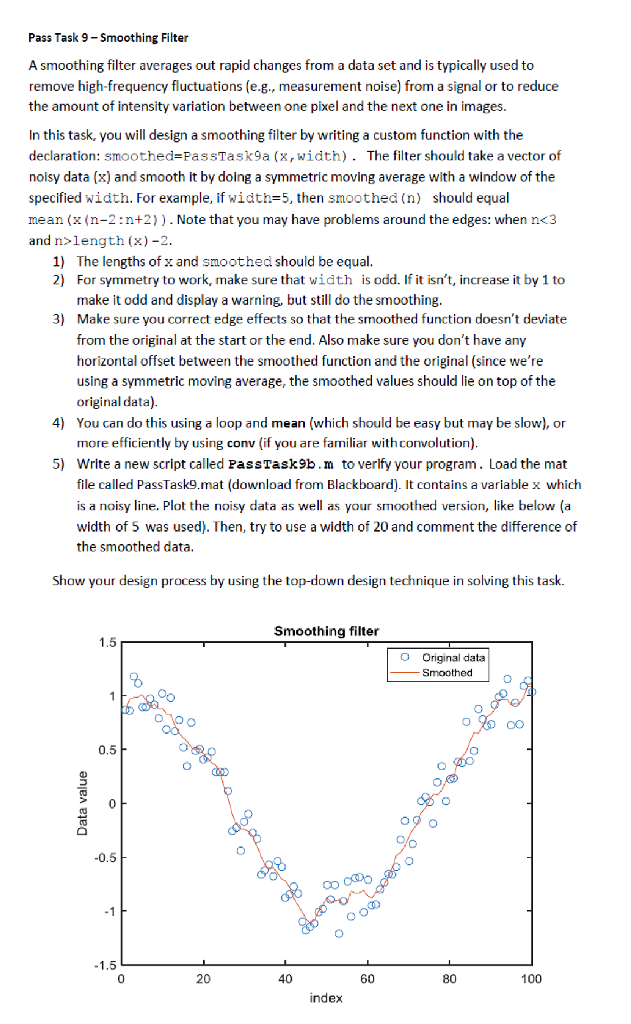
A smoothing filter averages out rapid changes from a data set and is typically used to remove high-frequency fluctuations (e.g., measurement noise) from a signal or to reduce the amount of intensity variation between one pixel and the next one in images. In this task, you will design a smoothing filter by writing a custom function with the declaration: smoothed = PassTask9a (x, width). The filter should take a vector of noisy data (x) and smooth it by doing a symmetric moving average with a window of the specified width. For example, if width = 5, then smoothed (n) should equal mean (x (n - 2: n + 2)). Note that you may have problems around the edges: when n length (x) - 2. 1) The lengths of x and smoothed should be equal. 2) For symmetry to work, make sure that width is odd. If it isn't, increase it by 1 to make it odd and display a warning, but still do the smoothing. 3) Make sure you correct edge effects so that the smoothed function doesn't deviate from the original at the start or the end. Also make sure you don't have any horizontal offset between the smoothed function and the original (since we're using a symmetric moving average, the smoothed values should lie on top of the original data). 4) You can do this using a loop and mean (which should be easy but may be slow), or more efficiently by using conv (if you are familiar with convolution). 5) Write a new script called PassTask9b.m to verify your program. Load the mat file called PassTask9.mat (download from Blackboard). It contains a variable x which is a noisy line. Plot the noisy data as well as your smoothed version, like below (a width of 5 was used). Then, try to use a width of 20 and comment the difference of the smoothed data. Show your design process by using the top-down design technique in solving this task