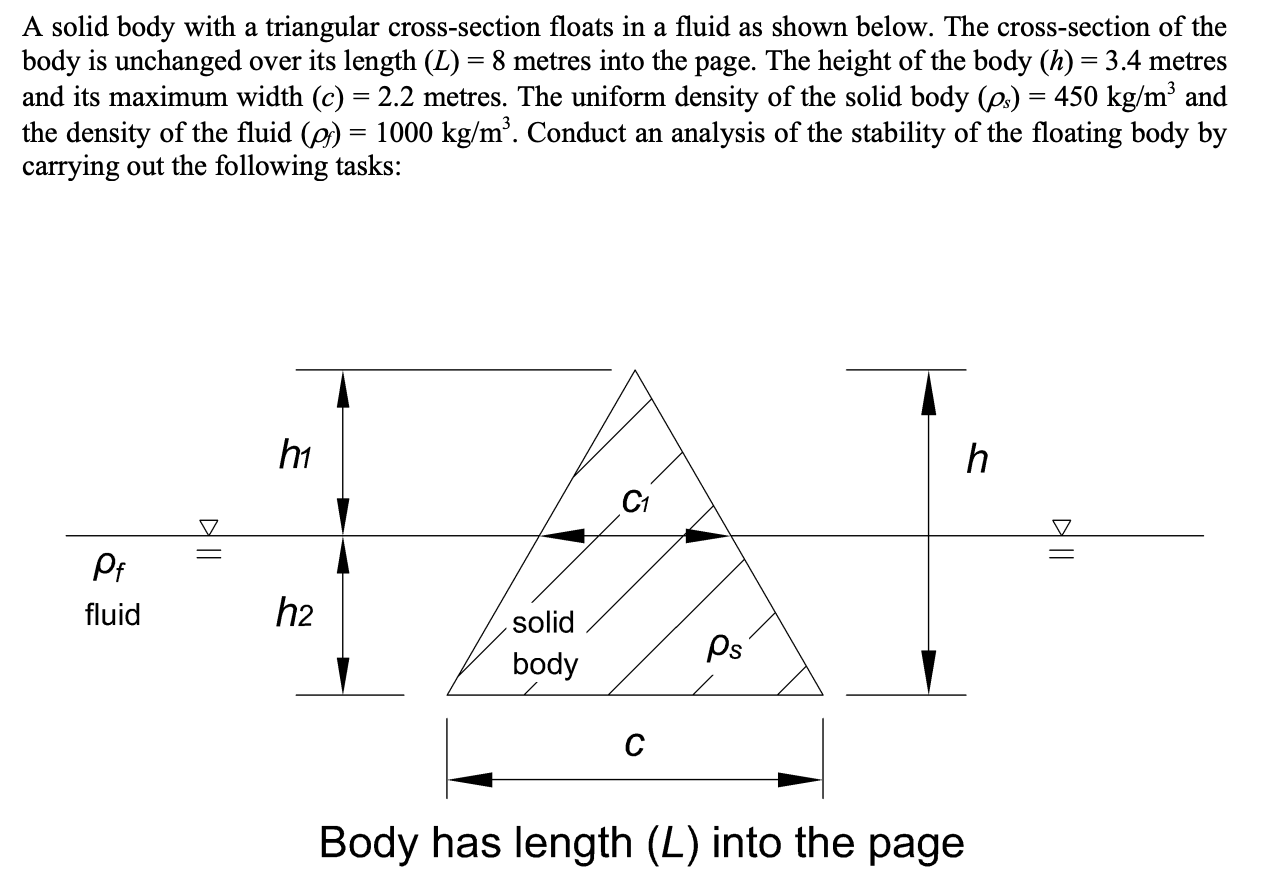
A solid body with a triangular cross$-$section floats in a fluid as shown below. The cross$-$section of the $2($d$)$: Noting that the submerged volume can be written as the difference between the total

volume of the floating object and the volume of the floating body above the free surface,

determine the value of $h_{\text{I}}$ in the figure above in metres. Hint: you might find the concept of

similar triangles usefiul here

Note: If you are unable to complete this part of the question, you can assume $h_l=2\mathrm{.}0$ and

proceed with the remainder of the question.

$2($e$)$: Determine the submerged depth $(h_2)$ of the floating object in metres:

$2($f$)$: Determine the width of the triangle $(c_l)$ at the waterline cross$-$section $($in metres$)$: $2($g$)$: Noting that the distance $(h_{\text{c}\text{e}\text{n}\text{t}\text{r}\text{o}\text{i}\text{d}})$ from the base of the floating object to the centroid of

the submerged volume can be written as:

$h_{\text{c}\text{e}\text{n}\text{t}\text{r}\text{o}\text{i}\text{d}}=h_2\frac{[\frac{c}{3}+\frac{2c_1}{3}]}{[c+c_1]}$

Determine the distance $($GB$)$ between the centre of gravity $(G)$ and the centre of buoyancy

$($B$)$ of the floating bodv $($in metres$)$:

$A{l}^2$

$2($h$)$: Determine the second moment of area about the waterline cross$-$section of the body $($in

$m^4).$ Note: Adopt the combination of $L$ and $c_l$; that generates the smallest second moment

of area. This is because the smallest second moment of area is critical in terms of stability.

$2($i$)$: Determine the distance $($BM$)$ between the centre of buoyancy $($B$)$ and metacentre $($M$)$ in

metres:

$2($j$)$: Determine the metacentric height $($GM$)$ for the floating body in metres.

$2($k$)$: State the value of the metacentric height necessary for neutral stability $($in metres$)$: $2($c$)$: Determine the submerged volume of the body $($in $m^3)$:

Answer: $,0\mathrm{.}0135$

$2($d$)$: Determine the value of $h_l$ in the figure above in metres.

Answer: $2\mathrm{.}522$

Note: If you are unable to complete this part of the question, you can assume $h_l=2\mathrm{.}0$ and

proceed with the remainder of the question.

$2($e$)$: Determine the submerged depth $(h_2)$ of the floating object in metres:

$2($f$)$: Determine the width of the triangle $(c_r)$ at the waterline cross$-$section $($in metres$)$:

$2($g$)$: Determine the distance $($GB$)$ between the centre of gravity $(G)$ and the centre of buoyancy

$($B$)$ of the floating hodv $($in metres$)$:

$2($h$)$: Determine the second moment of area about the waterline cross$-$section of the body $($in

$m^4).$ Note: Adopt the combination of $L$ and $c_1$; that generates the smallest second moment

of area. This is because the smallest second moment of area is critical in terms of stability.

$2($i$)$: Determine the distance $($BM$)$ between the centre of buoyancy $($B$)$ and metacentre $($M$)$ in

metres:

$2($j$)$: Determine the metacentric height $($GM$)$ for the floating body in metres.

Answer: $,-0\mathrm{.}5000$

body is unchanged over its length $(L)=8$ metres into the page. The height of the body $(h)=3\mathrm{.}4$ metres

and its maximum width $(c)=2\mathrm{.}2$ metres. The uniform density of the solid body $({}_s)=450k\frac{g}{m^3}$ and

the density of the fluid $({}_f)=1000k\frac{g}{m^3}.$ Conduct an analysis of the stability of the floating body by

carrying out the following tasks: Answers are provided, just confused on the working and the steps to take for each question. Please solve the quesstions to arrive at the given answers :)