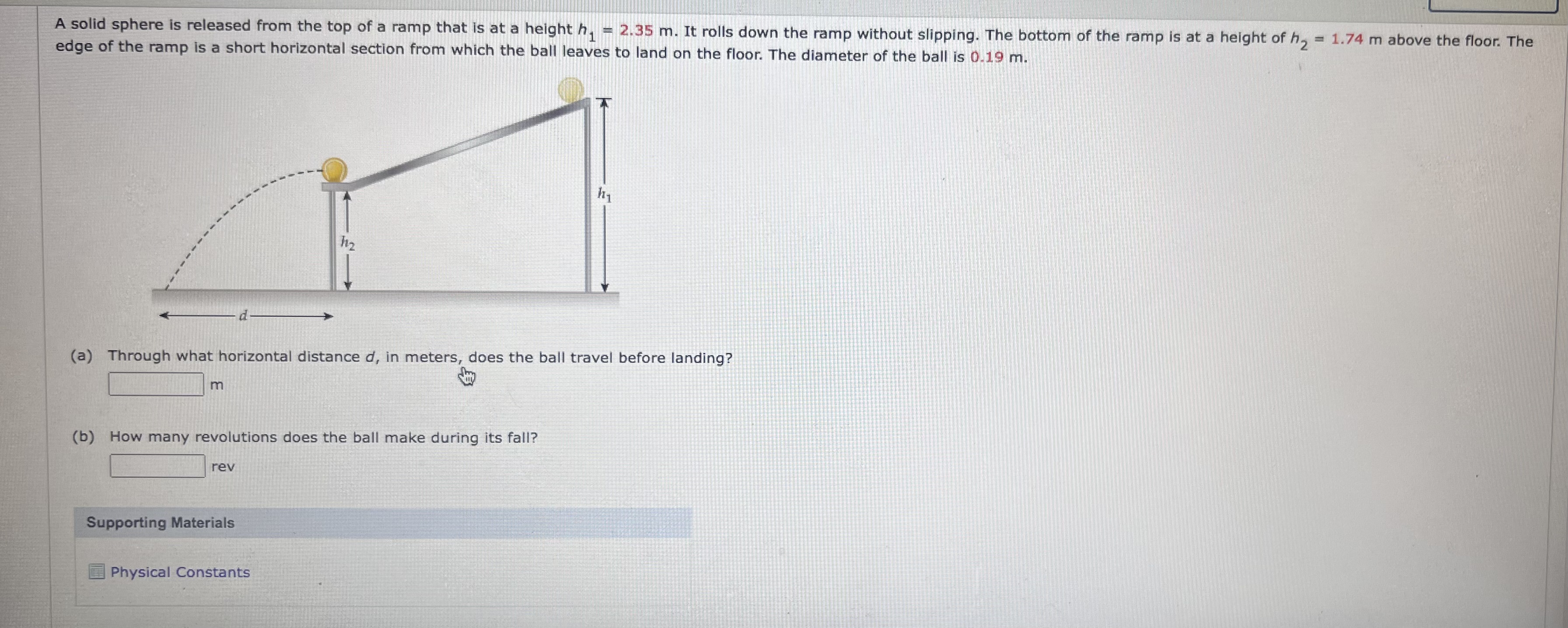
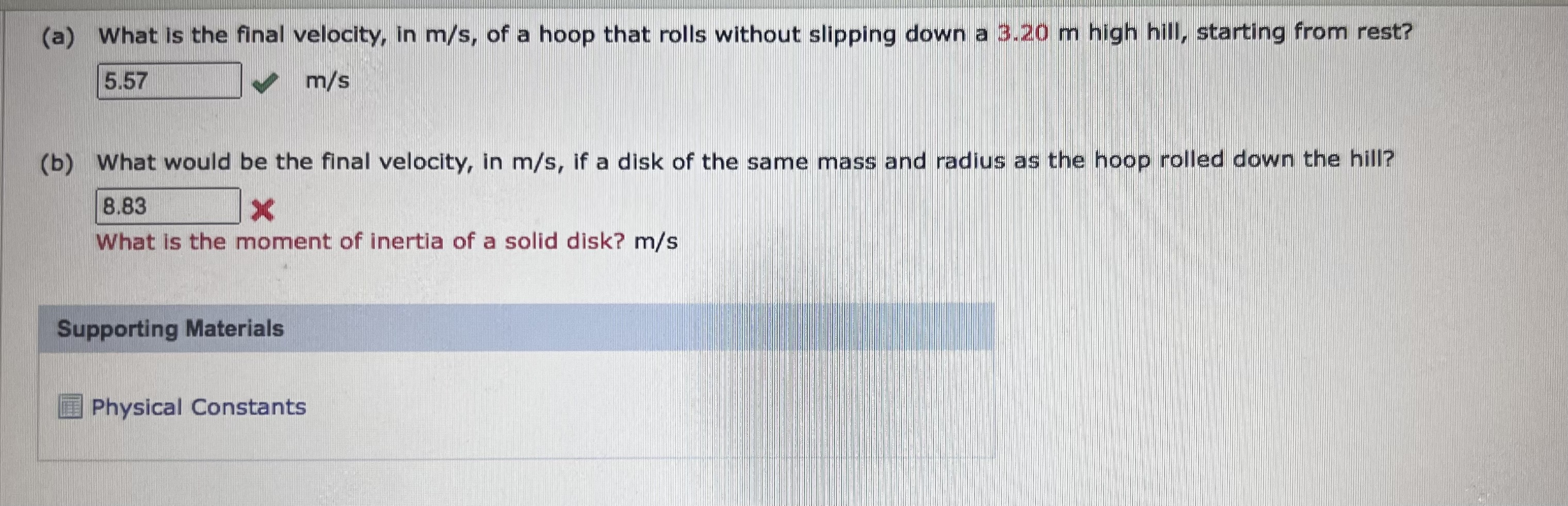
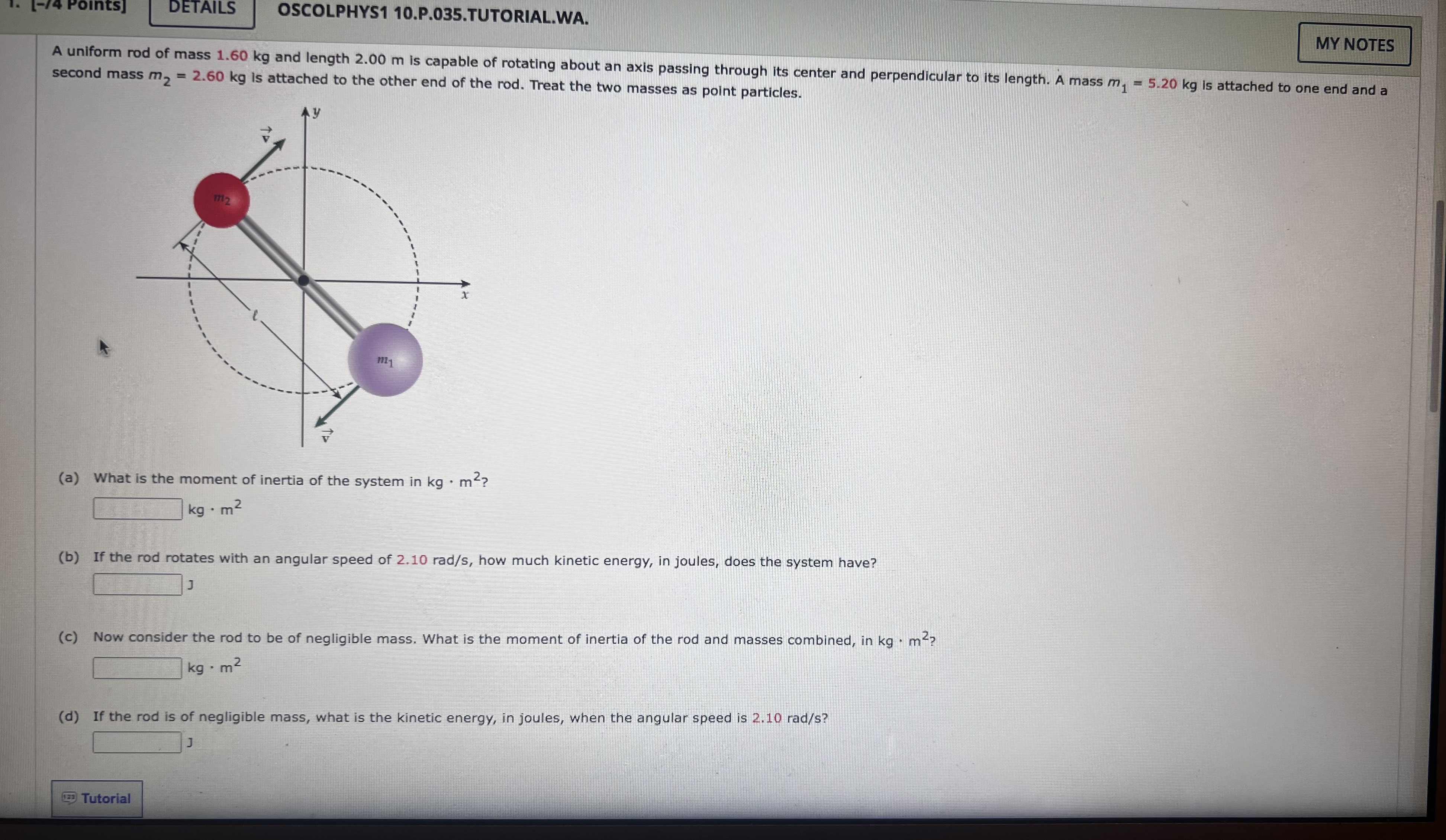
A solid sphere is released from the top of a ramp that is at a height h, - 2.35 m. It rolls down the ramp without slipping. The bottom of the ramp is at a height of h, = 1.74 m above the floor. The edge of the ramp is a short horizontal section from which the ball leaves to land on the floor. The diameter of the ball is 0.19 m. hz (a) Through what horizontal distance d, in meters, does the ball travel before landing? m (b) How many revolutions does the ball make during its fall? rev Supporting Materials Physical Constants(a) What is the final velocity, in m/s, of a hoop that rolls without slipping down a 3.20 m high hill, starting from rest? 5.57 m/s (b) What would be the final velocity, in m/s, if a disk of the same mass and radius as the hoop rolled down the hill? 8.83 x What is the moment of inertia of a solid disk? m/s Supporting Materials Physical ConstantsDETAILS OSCOLPHYS1 10.P.035.TUTORIAL.WA. MY NOTES A uniform rod of mass 1.60 kg and length 2.00 m is capable of rotating about an axis passing through its center and perpendicular to its length. A mass m, = 5.20 kg is attached to one end and a second mass my = 2.60 kg is attached to the other end of the rod. Treat the two masses as point particles. m2 1211 (a) What is the moment of inertia of the system in kg . my? kg . m 2 (b) If the rod rotates with an angular speed of 2.10 rad/s, how much kinetic energy, in joules, does the system have? (c) Now consider the rod to be of negligible mass. What is the moment of inertia of the rod and masses combined, in kg . m-? kg . m2 (d) If the rod is of negligible mass, what is the kinetic energy, in joules, when the angular speed is 2.10 rad/s? TutorialMY NOTES A meter stick has a mass of 0.24 kg and balances at its center. When a small chain is suspended from one end, the balance point moves 16.0 cm toward the end with the chain. Determine the mass of the chain. 510 X Determine a convenient place for the origin of the coordinate system. See if you can write an expression for the center of mass of the two objects in terms of known quantities and the mass of the chain and then solve for the mass of the chain. g Supporting Materials Physical Constants