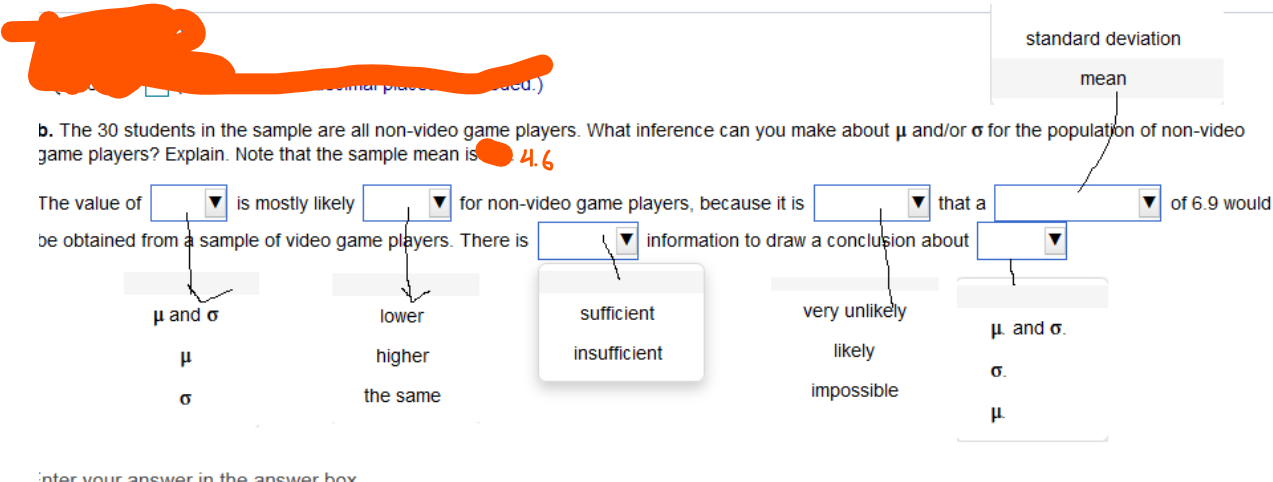
A study was designed to determine whether video game players are better than non-video game players at crossing the street when presented with distractions. Participants (college students) entered a street-crossing simulator. The simulatorwas designed to have cars traveling at various high rates of speed in both directions. During the crossing, the students also performed a memory task as a distraction. The researchers found that students who are video game players took an average of 4.4 seconds to cross the street, with a standard deviation of 0.6 seconds. Assume that the time, x, to cross the street for the population of video game players has p =4.4 and a = 0.6. Now oonsider a sample of 40 students and let 2 represent the sample mean time (in seconds) to cross the street in the simulator. Complete parts a and b below. a. Find P(i>4_6). PO} > 4.6) = (Round to three decimal places as needed.) standard deviation mean b. The 30 students in the sample are all non-video game players. What inference can you make about u and/or o for the population of non-video game players? Explain. Note that the sample mean is 4.6 The value of is mostly likely for non-video game players, because it is that a of 6.9 would be obtained from a sample of video game players. There is information to draw a conclusion about H and o lower sufficient very unlikely H. and o. higher insufficient likely O. o the same impossible