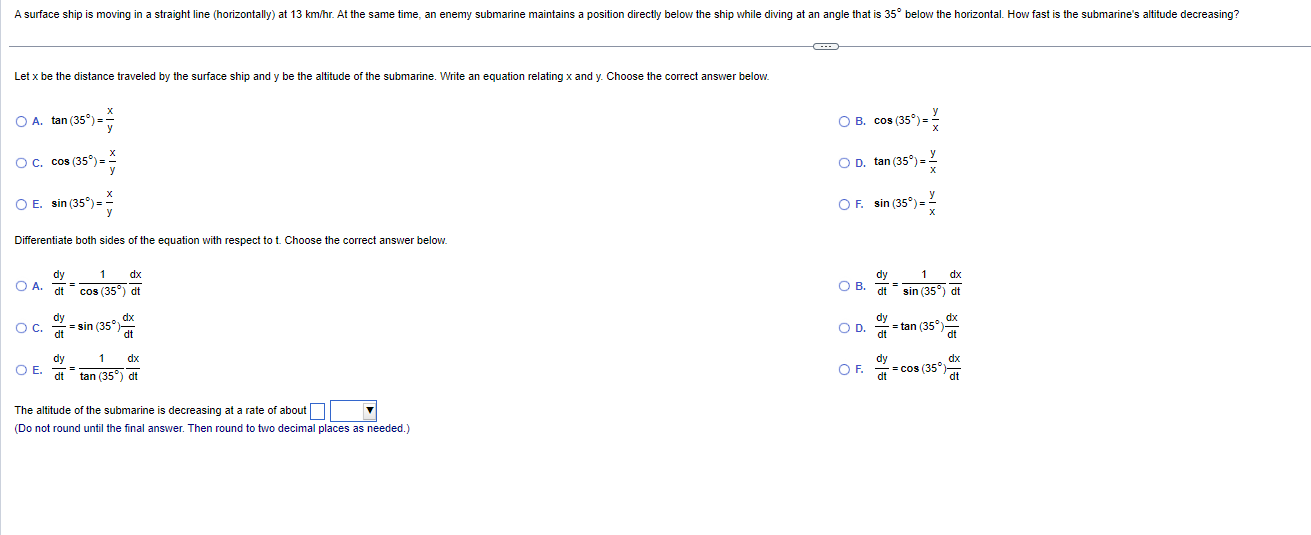
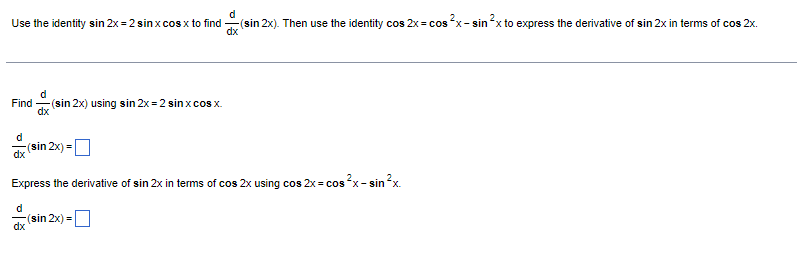
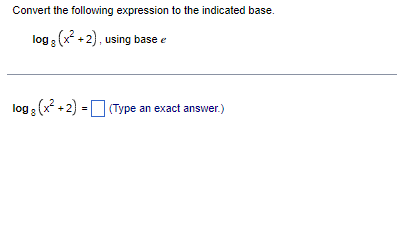
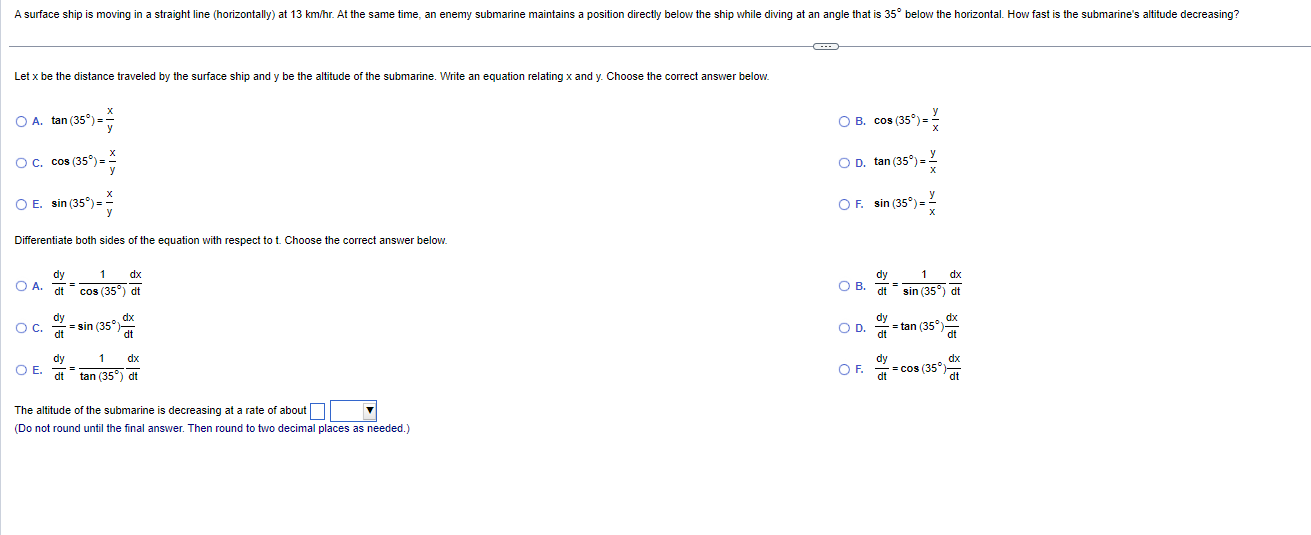
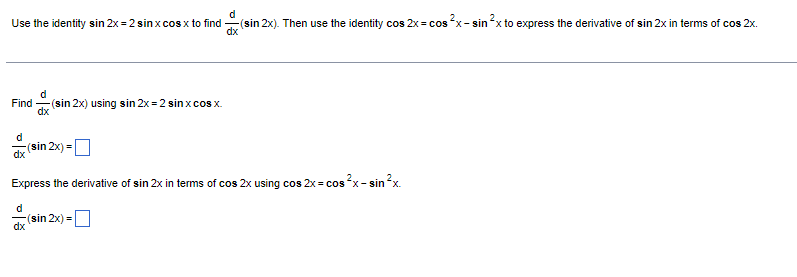
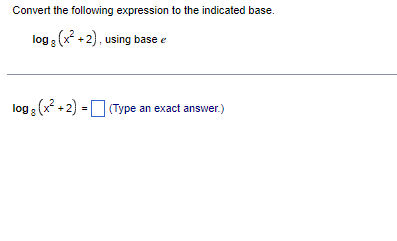
A surface ship is moving in a straight line (horizontally) at 13 km/hr. At the same time, an enemy submarine maintains a position directly below the ship while diving at an angle that is 35" below the horizontal. How fast is the submarine's altitude decreasing? Let x be the distance traveled by the surface ship and y be the altitude of the submarine. Write an equation relating x and y. Choose the correct answer below. O A. tan (35 ) = = O B. cos (35' ) = = O C. cos (35") = = O D. tan (359) = _ O E. sin (35") = OF. sin (35') = = Differentiate both sides of the equation with respect to t. Choose the correct answer below. dy 1 dx 1 dx O A. dt cos (35" ) dt O B. dy sin (35) dt O c. - = sin (35)- dx =tan (353)- dx dt OD. - dy dx OF. dx O E. dt tan (35) dt = cos (35 )t The altitude of the submarine is decreasing at a rate of about] (Do not round until the final answer. Then round to two decimal places as needed.)Using the graph of f shown below, find three intervals on which f is one-to-one, making each interval as large as possible. The intervals on which f is one-to-one are ( - co, . [. , and . co)- (Simplify your answers.)d Use the identity sin 2x = 2 sin x cos x to find -(sin 2x). Then use the identity cos 2x= cos ~x - sin x to express the derivative of sin 2x in terms of cos 2X. dx d Find dx - (sin 2x) using sin 2x = 2 sin x cos x. dx - (sin 2x) = Express the derivative of sin 2x in terms of cos 2x using cos 2x = cos -x - sin -x. (sin 2x) = dxConvert the following expression to the indicated base. log 8 + 2) , using base e (x2 +2) = 0 (Type an exact answer.)