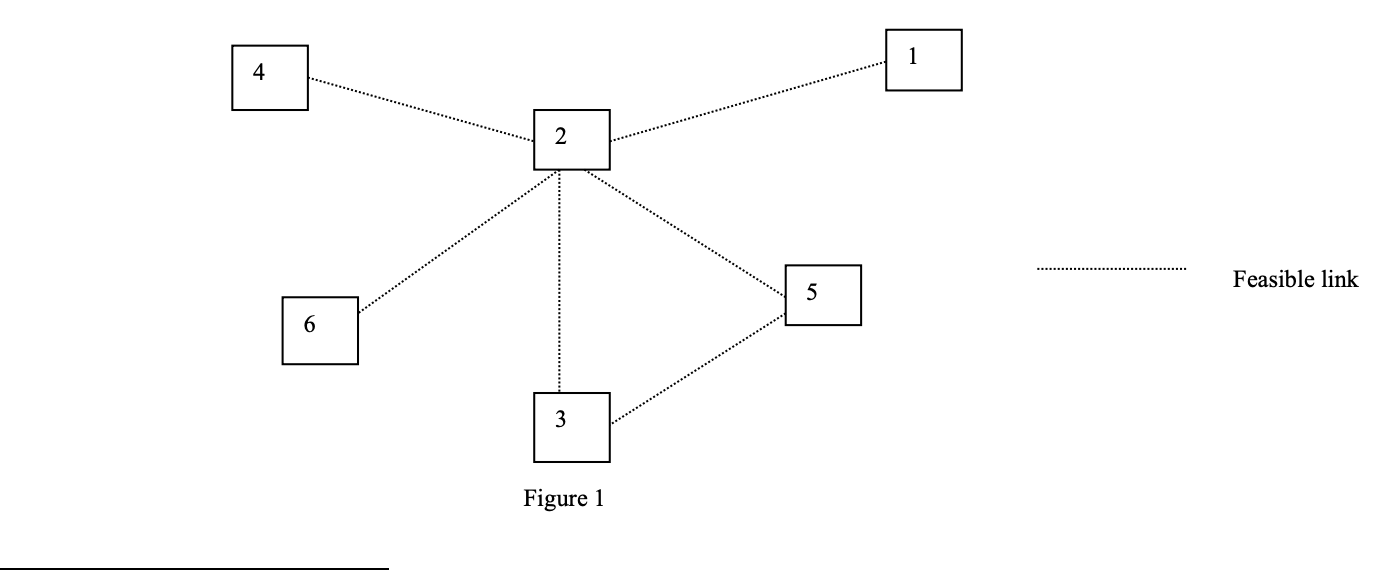
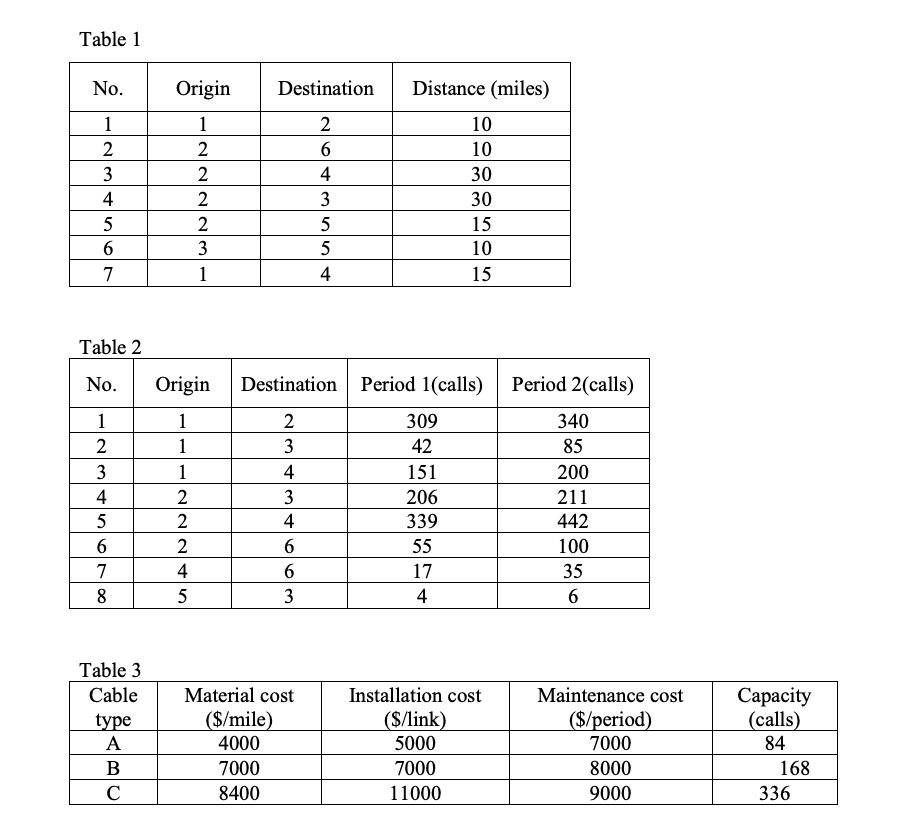
A telecommunications company operates a network that includes many medium to large metropolitan area networks (MANs). Each MAN consists of wire centers (nodes) interconnected by capacitated fiber-optic cables along the feasible network links. Local calls are carried to a wire center near the point of origin and then routed along consecutive links to the destination wire center near the final destination. The network structure for this problem has six nodes and six feasible links (Figure 1) with the distances between nodes given in Table 1. The maximum call demand between selected nodes is forecasted over two periods as shown in Table 2. The types of fiber-optic cables available to be installed along the links are listed in Table 3 which contains their costs and capacities. A call can be carried through any path, but it cannot use more than 3 links. All cable types allow calls in both directions, i.e., cable between nodes i and j can handle calls from j to i as well as from i to j. Cable can be installed along any link at the start of either period 1 or 2. There is no restriction on the number of cables between any two nodes. When cables are installed between two selected nodes in a period, the installation cost will be incurred in that period. The maintenance cost for each cable type will be incurred in period 1 and period 2 if the links are installed in period 1. Maintenance costs will be incurred only in period 2 if the links are installed in period 2. Installation and maintenance costs do not depend on the number of cables installed. For example, if two type B cables are installed in period 1 between nodes 2 and 6, then an installation cost of $7,000 will be incurred in period 1 and no installation cost for those cables will occur in period two. A maintenance cost of $8000 will be incurred in each period for those cables. Material costs depend, of course, on the length and number of cables installed.

a.) Formulate the problem as an integer linear program for minimizing the costs over two periods.

b.) Develop a suitable LINGO or LINDO model and find an optimal solution that minimizes the total cost. Give a summary of the solution.

c.) Suppose that link 1-4 is now feasible, modify your integer linear program in a).

4 2 Feasible link 5 6 3 Figure 1 Table 1 No. Origin Destination Distance (miles) 1 2 3 4 5 6 7 1 2 2 2 2 3 1 uu wa 2 6 4 3 5 5 4 10 10 30 30 15 10 15 Table 2 No. Origin Destination Period 1(calls) Period 2(calls) 1 2 3 4 5 6 7 8 ANNN 1 1 1 2 2 2 4 5 2 3 4 3 4 6 6 3 309 42 151 206 339 55 17 4 340 85 200 211 442 100 35 6 Table 3 Cable type A B Material cost ($/mile) 4000 7000 8400 Installation cost ($/link) 5000 7000 11000 Maintenance cost ($/period) 7000 8000 9000 Capacity (calls) 84 168 336