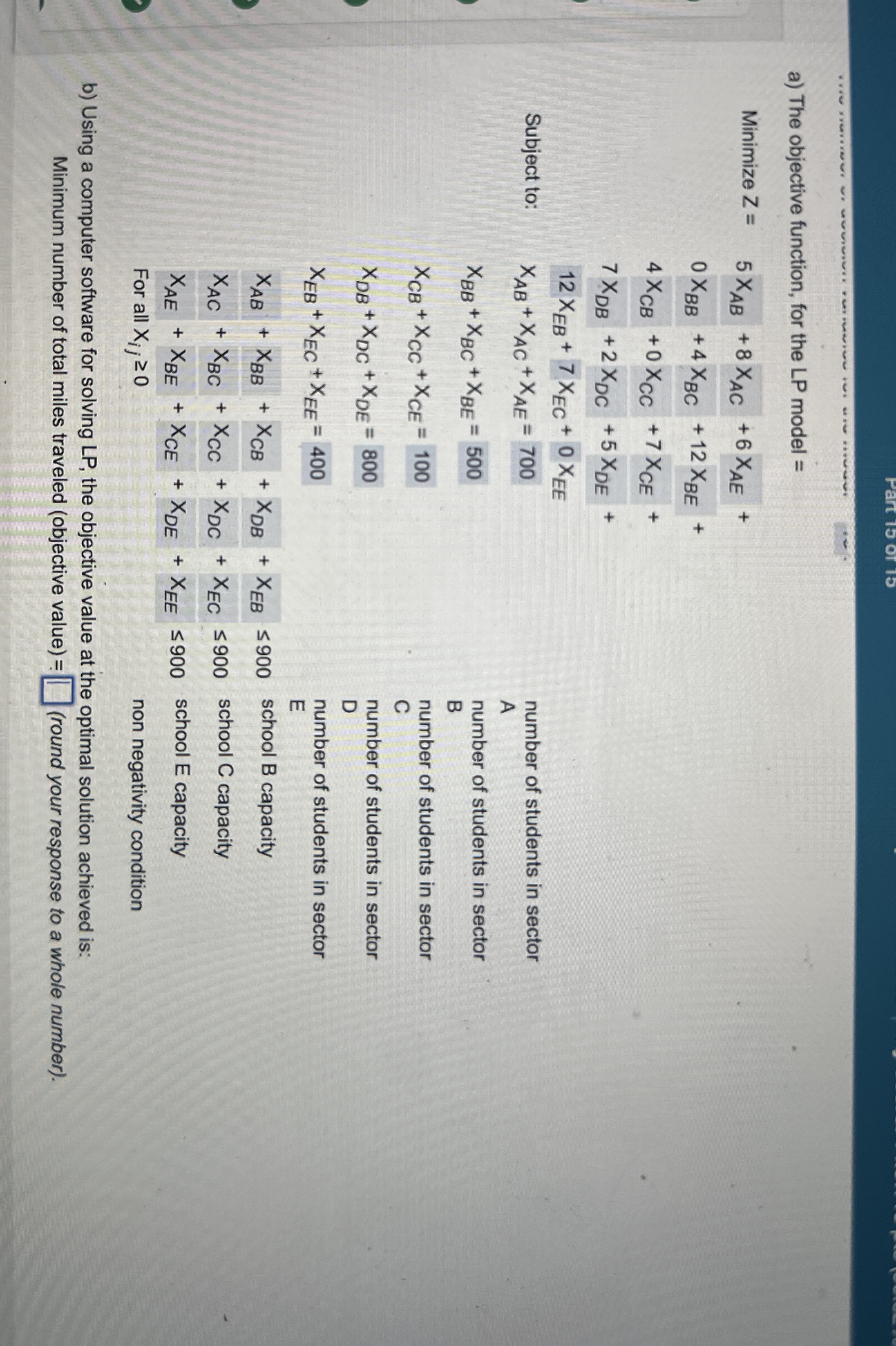
a$)$ The objective function, for the LP model $=$

Minimize $Z=$

$5x_{AB}+8x_{AC}+6x_{AE}+$

$0x_{BB}+4x_{BC}+12x_{BE}+$

$4x_{CB}+0x_{CC}+7x_{CE}+$

$7x_{DB}+2x_{DC}+5x_{DE}+$

$12x_{EB}+7x_{EC}+0x_{EE}$

Subject to:

$x_{AB}+x_{AC}+x_{AE}=700$

$x_{BB}+x_{BC}+x_{BE}=500$

$x_{CB}+x_{CC}+x_{CE}=100$

$x_{DB}+x_{DC}+x_{DE}=800$

$x_{EB}+x_{EC}+x_{EE}=400$

$x_{AB}+x_{BB}+x_{CB}+x_{DB}+x_{EB}900$

$x_{AC}+x_{BC}+x_{CC}+x_{DC}+x_{EC}900$

$x_{AE}+x_{BE}+x_{CE}+x_{DE}+x_{EE}900$

For all $x_{ij}0$

number of students in sector

A

number of students in sector

B

number of students in sector

C

number of students in sector

D

number of students in sector

E

school B capacity

school C capacity

school E capacity

non negativity condition

b$)$ Using a computer software for solving LP$,$ the objective value at the optimal solution achieved is:

Minimum number of total miles traveled $($objective value$)=($round your response to a whole number$).$The Hills County, Michigan, superintendent of education is responsible for assigning students to the three high schools in his county. He recognizes the need to bus a certain number of students, for several sectors$,A-E,$ of the county are beyond walking distance to a school. The superintendent partitions the county into five geographic sectors as he attempts to establish a plan that will minimize the total number of student miles traveled by bus. He also recognizes that if a student happens to live in a certain sector and is assigned to the high school in that sector, there is no need to bus him because he can walk to school. The three schools are located in sectors B$,$ C$,$ and E$.$

The accompanying table reflects the number of high$-$school$-$age students living in each sector and the distance in miles from each sector to each school:

Each high school has a capacity of $900$ students.

You have been asked to develop. a linear programming model so as to minimize the total number of student miles traveled bif bus.

Decision variable $x_{ij}$ : Number of students living in sector i traveling to school located in sector $j.$

The number of decision variables for the model $=15.$

a$)$ The objective function, for the LP model $=$

Minimize $Z=5x_{AB}+8x_{AC}+6x_{AE}+$

$0x_{BB}+4x_{BC}+12x_{BE}+$

$4x_{CB}+0x_{CC}+7x_{CE}+$

a$)$ The objective function, for the LP model $=$

Minimize $Z=5x_{AB}+8x_{AC}+6x_{AE}+$

$0x_{BB}+4x_{BC}+12x_{BE}+$

$4x_{CB}+0x_{CC}+7x_{CE}+$

$7x_{DB}+2x_{DC}+5x_{DE}+$

$12x_{EB}+7x_{EC}+0x_{EE}$

Subject $to$: $x_{AB}+x_{AC}+x_{AE}=700$

$x_{BB}+x_{BC}+x_{BE}=500$

$x_{CB}+x_{CC}+x_{CE}=100$

$x_{DB}+x_{DC}+x_{DE}=800$

$x_{EB}+x_{EC}+x_{EE}=400$

$x_{AB}+x_{BB}+x_{CB}+x_{DB}+x_{EB}900$ school $B$ capacity

$x_{AC}+x_{BC}+x_{CC}+x_{DC}+x_{EC}900$ school $C$ capacity

$x_{AE}+x_{BE}+x_{CE}+x_{DE}+x_{EE}900$ school $E$ capacity

For all $x_{ij}0$ non negativity condition

b$)$ Using a computer software for solving LP$,$ the objective value at the optimal solution achieved is: Minimum number of total miles traveled $($objective value$)=.$

number of students in sector

A

number of students in sector

B

number of students in sector

C

number of students in sector

D

number of students in sector

E

school B capacity

school C capacity

school E capacity

non negativity conditi