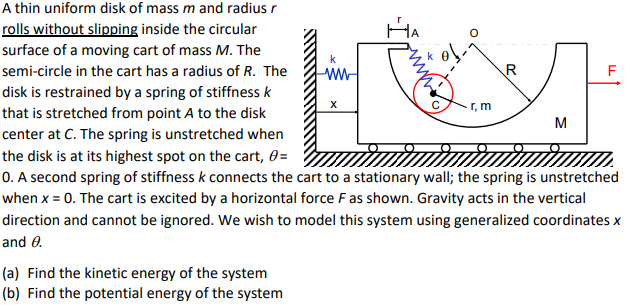
Question: A thin uniform disk of mass ( m ) and radius ( r ) rolls without slipping inside the circular surface
A thin uniform disk of mass m and radius r rolls without slipping inside the circular surface of a moving cart of mass M The semicircle in the cart has a radius of R The disk is restrained by a spring of stiffness k that is stretched from point A to the disk center at C The spring is unstretched when the disk is at its highest spot on the cart, theta A second spring of stiffness k connects the cart to a stationary wall; the spring is unstretched when x The cart is excited by a horizontal force F as shown. Gravity acts in the vertical direction and cannot be ignored. We wish to model this system using generalized coordinates x and theta
a Find the kinetic energy of the system
b Find the potential energy of the system
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


