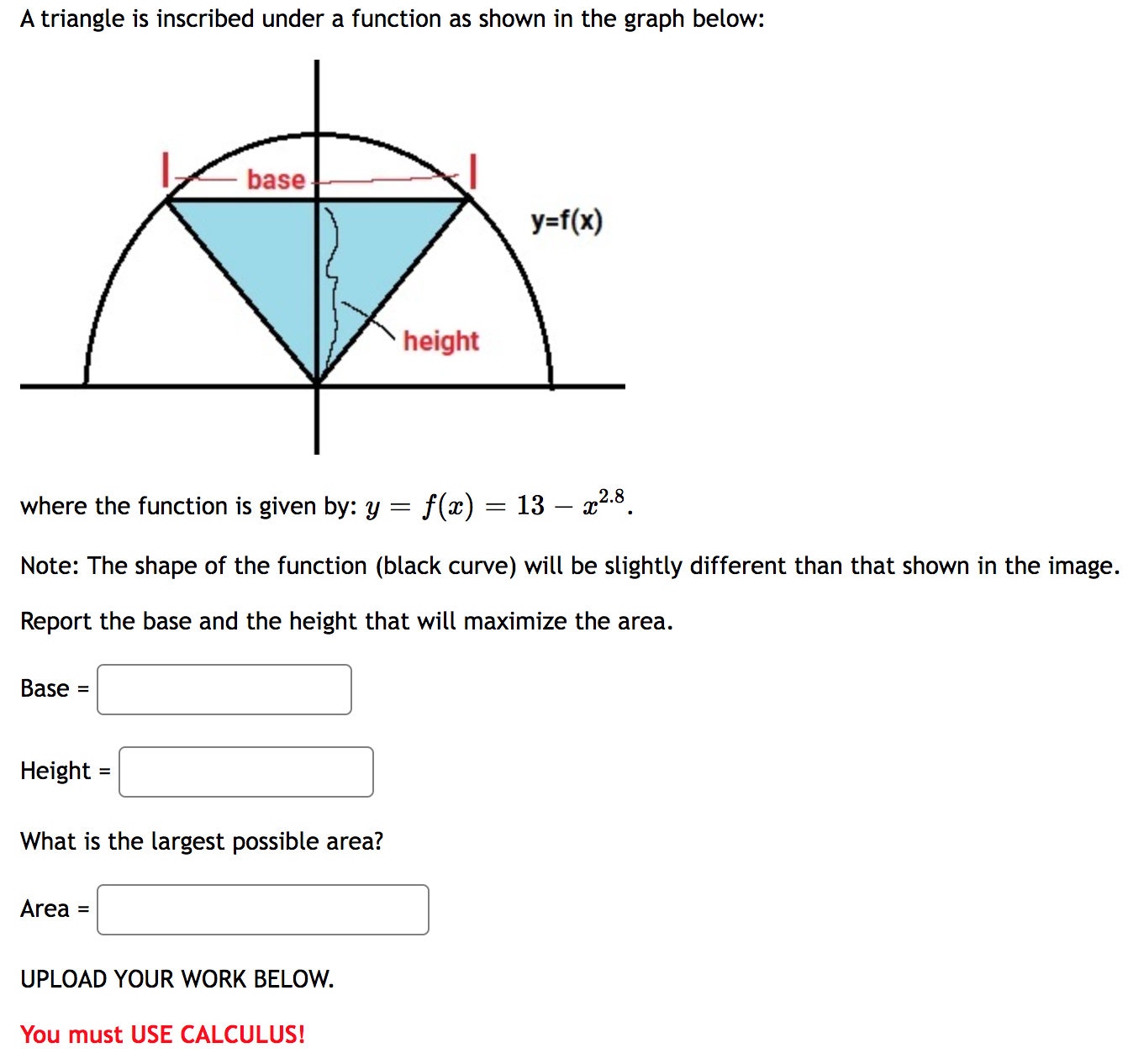
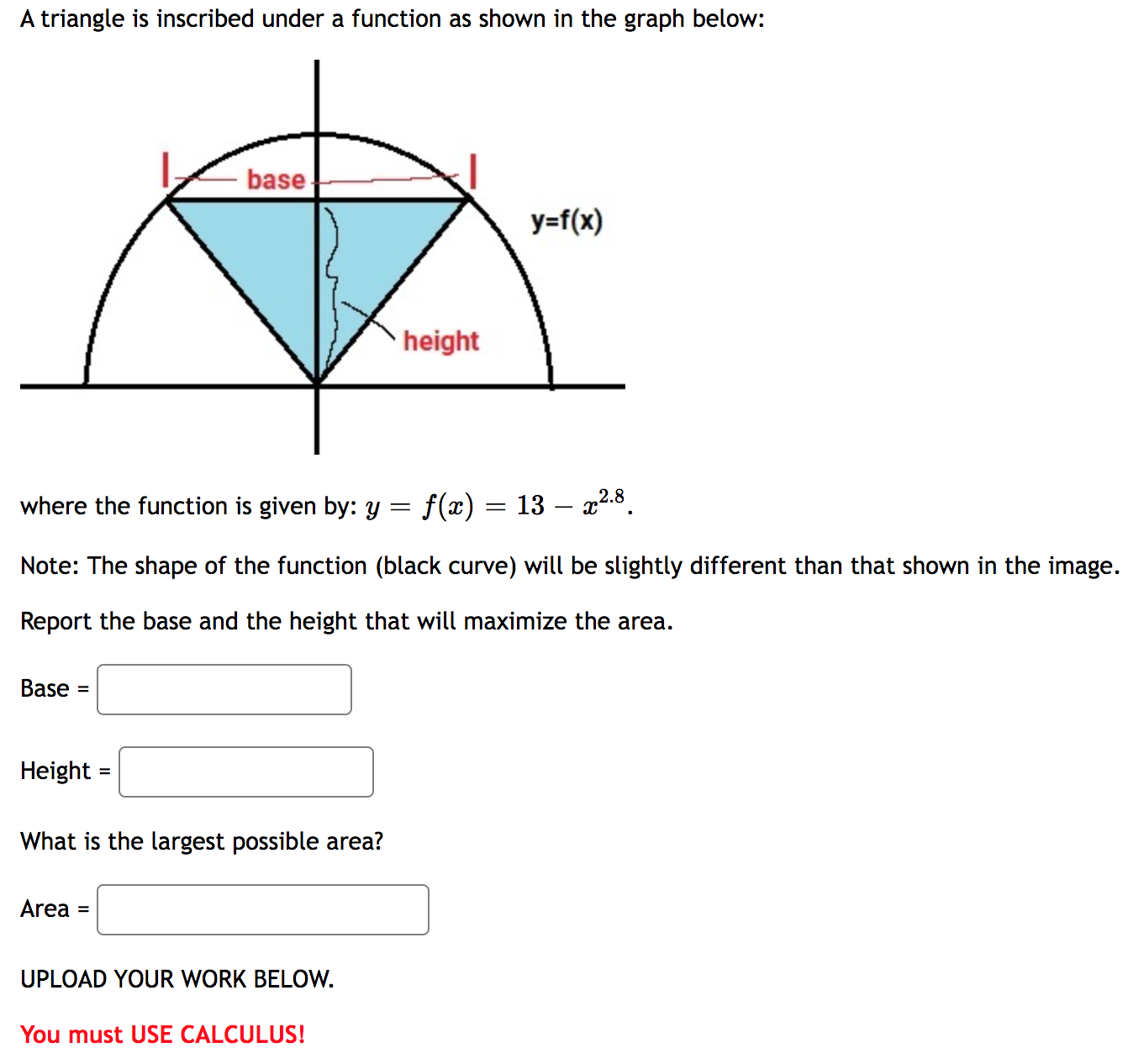
A triangle is inscribed under a function as shown in the graph below: where the function is given by: y = f(3) = 13 532's. Note: The shape of the function (black curve) will be slightly different than that shown in the image. Report the base and the height that will maximize the area. What is the largest possible area? UPLOAD YOUR WORK BELOW. You must USE CALCULUS! Make sure to show the following work: 1) Build the objective function 2) Find all critical values (make is clear you considered all possibilities -- where f'(x) = 0, f'(x) is undefined and endpoints for the domain 3) Use the Extreme Value Theorem, First Derivative Test or Second Derivative Test to determine which critical value is the maximum. 4) State your answer in a sentence (no units are given in this problem)