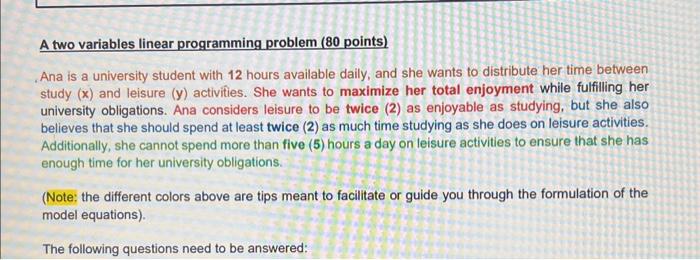
A two variables linear programming problem ( 80 points) . Ana is a university student with 12 hours available daily, and she wants to distribute her time between study (x) and leisure (y) activities. She wants to maximize her total enjoyment while fulfilling her university obligations. Ana considers leisure to be twice (2) as enjoyable as studying, but she also believes that she should spend at least twice (2) as much time studying as she does on leisure activities. Additionally, she cannot spend more than five (5) hours a day on leisure activities to ensure that she has enough time for her university obligations. (Note: the different colors above are tips meant to facilitate or guide you through the formulation of the model equations). The following questions need to be answered: 8. (5 points) What is the allowable increase of the coefficient accompanying leisure in the objective function (i.e., the coefficient equal to 2 in the objective function)? 9. (5 points) Explain the meaning of the number referenced in question 8 using the problem context