A unity amplitude square wave y(t) can be approximated by the following sum of three sine waves:

y ( t ) 4 ( sin ( x ) + 1 3 sin ( 3 x ) + 1 5 sin ( 5 x ) )

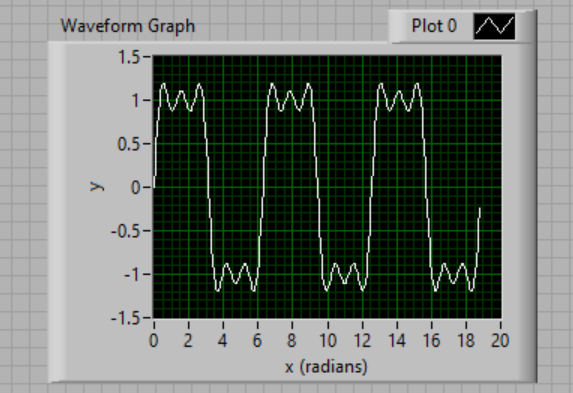
where x is in radians. Write a VI that evaluates this sum at 300 equally spaced x-values in the range from x = 0 to x = 6 (i.e., for three cycles of the first sine function in the sum) and then plots the resulting y vs. x on a Waveform Graph, whose x-axis is calibrated in radians. When the VI is run, it should produce the front panel plot shown next.

Suggested icon: Sine, Compound Arithmetic, Pi.

in lab view

Waveform Graph Plot 0 M 1.5- BA 1- WW 0.5-1 IN UVU -1.5--TTT 0 2 4 6 14 16 18 20 8 10 12 x (radians) Waveform Graph Plot 0 M 1.5- BA 1- WW 0.5-1 IN UVU -1.5--TTT 0 2 4 6 14 16 18 20 8 10 12 x (radians)