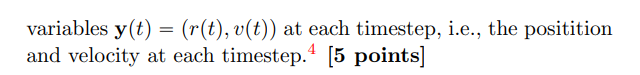
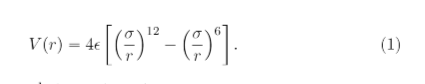
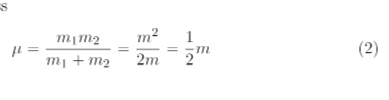
(a) Use Euler's method to perform the simulation of the vibrations of the argon dimer. Include all your functions in in a file 1jpy (which may itself import integrators.py if necessary). (i) Create a function dimer_md (r0, v0, t_max =10,dt=1e3, mass=1) in 1jpy that integrates Newton's equations of motion Eq. 3 for r(t) for the force Eq. 4 with the Euler integrator. You can use the implementation of the force function 1j.F_LJ() that is provided in 1j py. The dimer_md() function should take the initial distance of the atoms r0 (in nm ) and initial relative velocity v0 (in nm/ps ) as well as the maximum time tmax, the integration timestep t, and the mass as input and return a tuple consisting of ( t,y ). t is a numpy array of all the times t and y is a numpy array consisting of the ODE standard form of the dependent variables y(t)=(r(t),v(t)) at each timestep, i.e., the positition and velocity at each timestep. 4 [5 points] V(r)=4[(r)12(r)6] =m1+m2m1m2=2mm2=21m dt2d2r=1F(r) F=drdV(r) (a) Use Euler's method to perform the simulation of the vibrations of the argon dimer. Include all your functions in in a file 1jpy (which may itself import integrators.py if necessary). (i) Create a function dimer_md (r0, v0, t_max =10,dt=1e3, mass=1) in 1jpy that integrates Newton's equations of motion Eq. 3 for r(t) for the force Eq. 4 with the Euler integrator. You can use the implementation of the force function 1j.F_LJ() that is provided in 1j py. The dimer_md() function should take the initial distance of the atoms r0 (in nm ) and initial relative velocity v0 (in nm/ps ) as well as the maximum time tmax, the integration timestep t, and the mass as input and return a tuple consisting of ( t,y ). t is a numpy array of all the times t and y is a numpy array consisting of the ODE standard form of the dependent variables y(t)=(r(t),v(t)) at each timestep, i.e., the positition and velocity at each timestep. 4 [5 points] V(r)=4[(r)12(r)6] =m1+m2m1m2=2mm2=21m dt2d2r=1F(r) F=drdV(r)