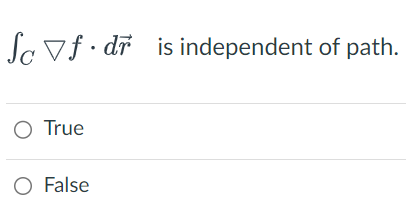
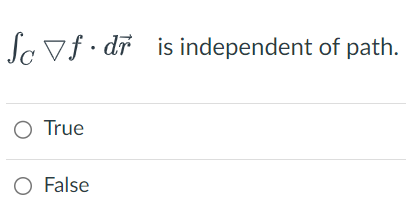
A vector field F is called conservative if there exists a function f such that F = O the gradient of f O the curl of f Of(x,y) O the line integral of fIn a conservative vector field, the work done around a closed path isSuppose the line integral , F . dr = -3 , then ( F . dr =So Vf . dr is independent of path. O True O FalseThe proof of the FToLI (Fundamental Theorem of Line Integrals) used which of the following? You may select one or more answers. O Fundamental Theorem of Calculus O Chain Rule for Multivariable Functions O Squeeze Theorem O Green's Theorem O Intermediate Value Theorem O Absolute Value Theorem O Product Rule for derivatives