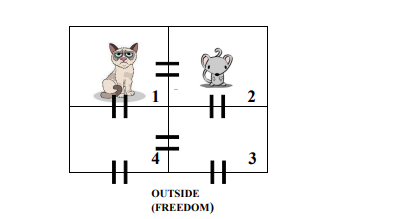
A very hungry cat, TOM, is placed in compartment $1$ and a mouse, named

JERRY, in compartment $2.$ Compartments are connected to each other, as shown above.

Although, JERRY may move between compartments, TOM is too big to fit through the

passages. Assume JERRY makes one move each minute. When JERRY makes a move,

assume that he picks a passage at random and moves to the adjacent compartment. That is$,$

if there are $$ passages, the probability that JERRY picks any given passage is $1/.$ If

JERRY enters to the compartment $1,$ the cat, TOM, eats him. On the other hand, if JERRY

leaves the maze he got his freedom and never returns back to the maze.

$2$

a$.$ Model the situation as a Markov Chain. Describe the states and write the Markov

transition matrix and draw the probability transition diagram.

b$.$ What is the probability that Jerry will be in compartments $3,4$ and $3$ after the first

move, second move and third move, respectively.

c$.$ Given the Jerry is in compartment $3$ after the third move, what is the probability that

he will be in compartment $2$ after the fifth move? Given the Jerry is in compartment $1$

after the third move, what is the probability that he will be in compartment $2$ after the

fifth move?

d$.$ What is the probability that the movements of Jerry in the maze will end up in

compartment $1?$ What is the probability that Jerry will get his freedom?

e$.$ What is the expected number of moves until Jerry enters compartment $1$ or he leaves

the maze?