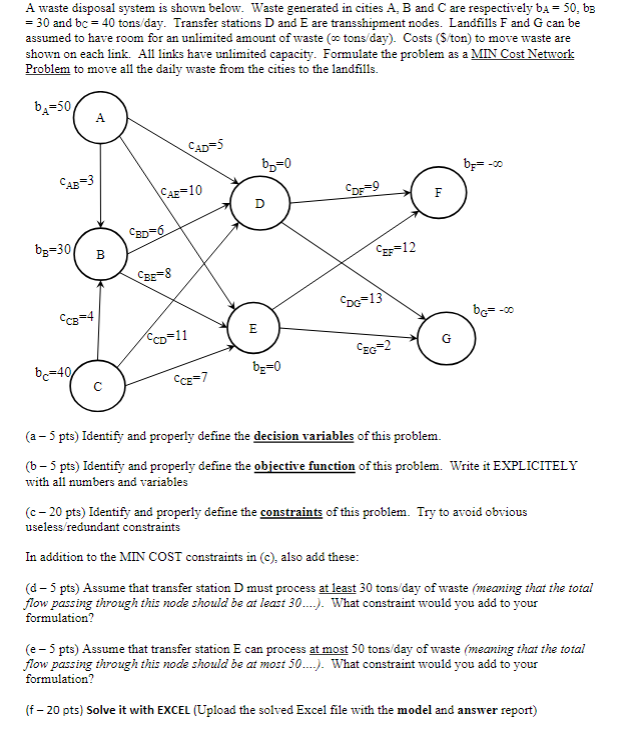
Question: A waste disposal system is shown below. Waste generated in cities ( A , B ) and ( C ) are
A waste disposal system is shown below. Waste generated in cities A B and C are respectively bA bB and b c tonsday Transfer stations D and E are transshipment nodes. Landfills F and G can be assumed to have room for an unlimited amount of waste infty tonsday Costs $ ton to move waste are shown on each link. All links have unlimited capacity. Formulate the problem as a MIN Cost Network Problem to move all the daily waste from the cities to the landfills.
a pts Identify and properly define the decision variables of this problem.
mathrmbmathrmpts Identify and properly define the objective function of this problem. Write it EXPLICITELY with all numbers and variables
mathrmcmathrmpts Identify and properly define the constraints of this problem. Try to avoid obvious uselessredundant constraints
In addition to the MIN COST constraints in c also add these:
d pts Assume that transfer station D must process at least tonsday of waste meaning that the total flow passing through this node should be at least ldots What constraint would you add to your formulation?
e pts Assume that transfer station E can process at most tonsday of waste meaning that the total flow passing through this node should be at most ldots What constraint would you add to your formulation?
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


