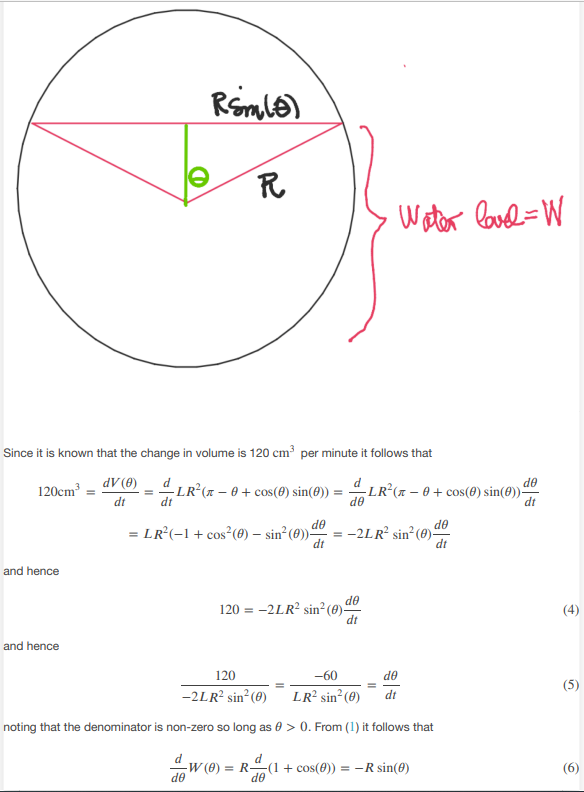
A water pipe with radius 1D cm and length 2t] m is lling with water at the rate of 12E! 1113 per minute. If both ends are sealed off and the pipe is parallel to the ground. how cuicldy is the water level in the pipe rising when the water level is 15 cm? What is wrong with the following "solution"? Find the error and produce a correct solution to this problem. Answer: Let us consider the more general problem when the pipe has radius R and length L since this is a case when the problem is simplied by avoiding concrete numbers. The accompanying diagram shows a cross section of the pipe with the green line being vertical and perpendicular to the side of the triangle. Let r denote time. Notice that a variable 6' has been introduced as well to represent the angle indicated and that .9 depends on time I. Let WEE) denote the water level as a function of H. The problems asks for dedr so implicit differentiation will be needed. The following represents W explicitly as a function of E: WM} = R + R cos(i} = RU + Ice-5(3)} [1} The area of the circle below the wateriine at height HF is equal to: c the area of the oirole l minus the pielike segment subtended between two radii forming an angle of as and the circumference of the oirole c plus the area of the triangle outlined in red. Hence the area A as a function of E is: sis} = x31 Esra: + airs cos[3}R sinESJu'EJ = slur - a + was} simian is) and multiplying this by the length of the pipe yields the volume V as a function of 3: FEB} = Lair: - a + were] 5111(3)} r3) RSmale) R Water love = W Since it is known that the change in volume is 120 cm per minute it follows that 120cm dv (@) dt dt " LR' (x - 0 + cos(0) sin(0)) = -LR'(x - 0 + cos(@) sin(@))- de = LR'(-1 + cos?(0) - sin?(@))- = -2LR2 sin-(@)- and hence 120 = -2LR2 sin- (0)- dt (4) and hence 120 -60 de -2LR2 sin (0) LR- sin (0) dt (5) noting that the denominator is non-zero so long as # > 0. From (1) it follows that d de -W(@) = R-(1 + cos(0)) = -R sin(@) (6)so that dW dw de -60 60 = - R sin(8) (7) dt de di LR2 sin- (0) LR sin(8) and so all that is needed is the value of sin(8) when the water level is 15 cm. Given that R = 10cm, this happens when R cos(0) = 5cm = R/2 or, in other words, when d = x/4. Since sin(x/4) = 1/v/2 it follows from (7) that at this height MP 60 601/2 dt LR/V2 LR and at the specific values given for L = 2000 and R = 10 it follows that the rate of change of the water level is 6012 = 3v2 x 10-3 2 x 104 or approximately 0.0042 cm per minute