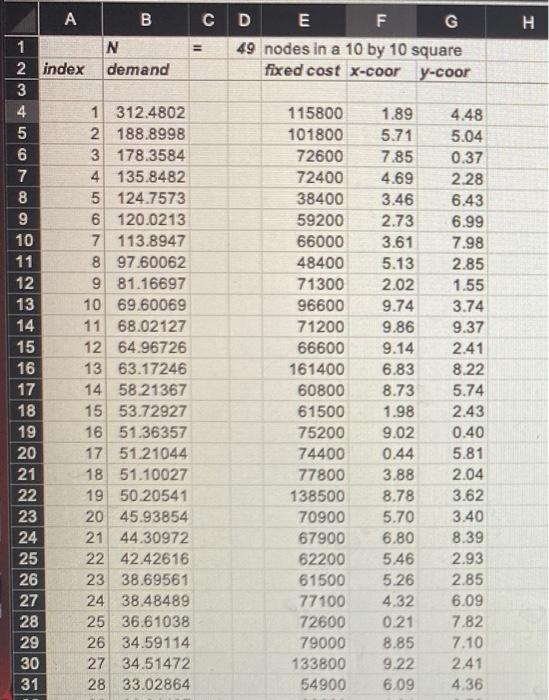
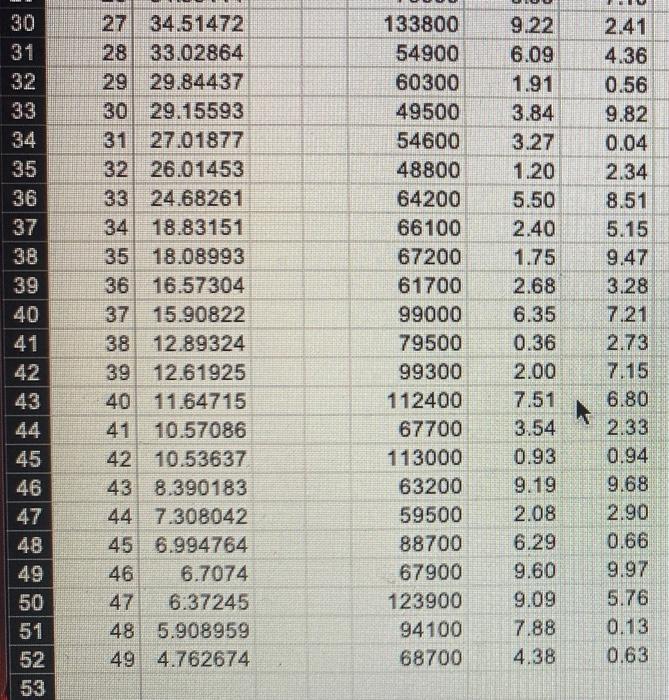
Question: a We now focus on the simpler uncapacitated fixed-charge facility location (UFL) problem. The attached Excel file data49points.xls contains the x- and y-coordinates of 49

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


